
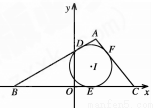
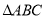 的内切圆与三边
的内切圆与三边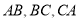 的切点分别为
的切点分别为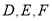 ,已知
,已知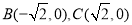 ,内切圆圆心
,内切圆圆心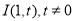 ,设点A的轨迹为R.
,设点A的轨迹为R.
(1)求R的方程;
(2)过点C的动直线m交曲线R于不同的两点M,N,问在x轴上是否存在一定点Q(Q不与C重合),使 恒成立,若求出Q点的坐标,若不存在,说明理由.
恒成立,若求出Q点的坐标,若不存在,说明理由.
(1) 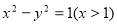 ;(2)存在
;(2)存在 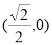
【解析】
试题分析:(1)根据切线长定理可得,AB-AC=2.根据双曲线的定义可得点A的轨迹是双曲线的一支,即可得到轨迹方程.
(2)因为 恒成立,通过化简可得等价结论,QC为∠MQN的角平分线.由直线MN垂直于x轴,显然存在点Q.当MN不垂直x轴时,依题意所求的结论等价转化于
恒成立,通过化简可得等价结论,QC为∠MQN的角平分线.由直线MN垂直于x轴,显然存在点Q.当MN不垂直x轴时,依题意所求的结论等价转化于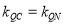 ,通过联立方程,利用韦达定理,即可求得点Q的横坐标.
,通过联立方程,利用韦达定理,即可求得点Q的横坐标.
试题解析:(1)设点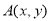 ,由题知|AB|-|AC|=|BE|-|CE|=|CE|+2|OE|-|CE|=2
,由题知|AB|-|AC|=|BE|-|CE|=|CE|+2|OE|-|CE|=2
根据双曲线定义知,点A的轨迹是以B、C为焦点,实轴长为2的双曲线的右支除去点E(1,0),故R的方程为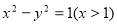
(2)设点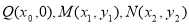 由(I)可知
由(I)可知


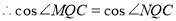
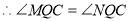 ①当直线
①当直线 轴时
轴时
点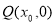 在
在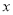 轴上任何一点处都能使得
轴上任何一点处都能使得 成立
成立
②当直线MN不与 轴垂直时,设直线
轴垂直时,设直线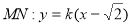
由 得
得
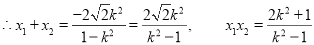
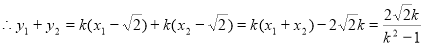

要使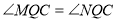 ,只需
,只需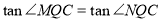 成立即
成立即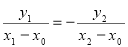 即
即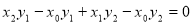
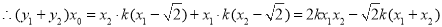
即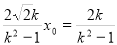 故
故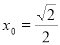 ,故所求的点Q的坐标为
,故所求的点Q的坐标为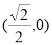 时
时
使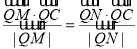 成立.
成立.
考点:1.圆的切线长定理.2.双曲线的性质.3.消元,韦达定理,运算能力等.4.等价转化的数学思想.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案科目:高中数学 来源:2013-2014学年江西省南昌市高三第二次模拟考试理科数学试卷(解析版) 题型:选择题
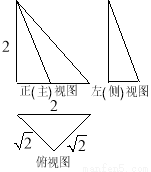
一几何体的三视图如图,该几何体的顶点都在球 的球面上,球
的球面上,球 的表面积是( )
的表面积是( )
A.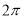 B.
B.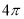 C.
C.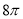 D.
D.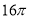
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省高三联合考试理科数学试卷(解析版) 题型:选择题
如果函数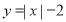 的图像与曲线
的图像与曲线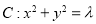 恰好有两个不同的公共点,则实数
恰好有两个不同的公共点,则实数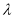 的取值范围是( )
的取值范围是( )
A.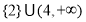 B.
B.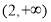 C.
C.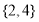 D.
D.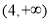
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省高三联合考试文科数学试卷(解析版) 题型:选择题
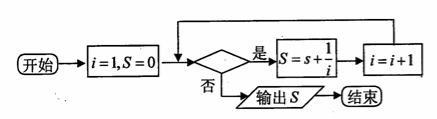
如图给出的计算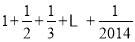 的值的一个程序框图,则判断框内应填入的条件是( )
的值的一个程序框图,则判断框内应填入的条件是( )
A.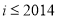 B.
B. C.
C.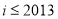 D.
D.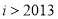
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省上饶市高三第二次模拟考试理科数学试卷(解析版) 题型:填空题
(不等式选讲题)对于任意实数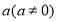 和
和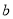 不等式
不等式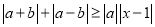 恒成立,则实数x的取值范围是_________.
恒成立,则实数x的取值范围是_________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省上饶市高三第二次模拟考试理科数学试卷(解析版) 题型:选择题
有红,蓝,黄,绿四种颜色的球各6个,每种颜色的6个球分别标有1、2、3、4、5、6,从中任取3个标号不同的球,这3个颜色互不相同且所标数字互不相邻的取法种数为( )
A.80 B.84 C.96 D.104
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省上饶市高三第二次模拟考试文科数学试卷(解析版) 题型:填空题
过双曲线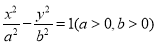 上任意一点P,作与实轴平行的直线,交两渐近线M,N两点,若
上任意一点P,作与实轴平行的直线,交两渐近线M,N两点,若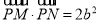 ,则该双曲线的离心率为____.
,则该双曲线的离心率为____.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省连云港市高三3月第二次调研考试理科数学试卷(解析版) 题型:解答题
设各项均为正数的数列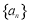 的前n项和为Sn,已知
的前n项和为Sn,已知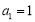 ,且
,且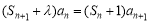 对一切
对一切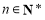 都成立.
都成立.
(1)若λ=1,求数列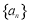 的通项公式;
的通项公式;
(2)求λ的值,使数列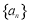 是等差数列.
是等差数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com