
【题目】已知函数g(x)= ![]() ,f(x)=g(x)﹣ax.
,f(x)=g(x)﹣ax.
(1)求函数g(x)的单调区间;
(2)若函数f(x)在(1,+∞)上是减函数,求实数a的最小值.
【答案】
(1)解:由已知函数g(x)的定义域为(0,1)∪(1,+∞),
且f(x)= ![]() ﹣ax(a>0),定义域为(0,1)∪(1,+∞),
﹣ax(a>0),定义域为(0,1)∪(1,+∞),
函数g′(x)= ![]() ,
,
当g′(x)>0时,x>e,当g′(x)<0时,0<x<1,1<x<e,
∴g(x)在(0,1),(1,e)递减,在(e,+∞)递增
(2)解:∵f(x)在(1,+∞)递减,
∴f′(x)= ![]() ﹣a≤0在(1,+∞)上恒成立,
﹣a≤0在(1,+∞)上恒成立,
∴x∈(1,+∞)时,f′(x)max≤0,
∵f′(x)=﹣ 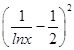 +
+ ![]() ﹣a,
﹣a,
∴当 ![]() =
= ![]() ,即x=e2时,f′(x)max=
,即x=e2时,f′(x)max= ![]() ﹣a,
﹣a,
∴ ![]() ﹣a≤0,于是a≥
﹣a≤0,于是a≥ ![]() ,
,
故a的最小值为 ![]()
【解析】(1)由函数g′(x)= ![]() ,得当g′(x)>0时,x>e,当g′(x)<0时,0<x<1,1<x<e,从而g(x)在(0,1),(1,e)递减,在(e,+∞)递增,(2)由f′(x)=
,得当g′(x)>0时,x>e,当g′(x)<0时,0<x<1,1<x<e,从而g(x)在(0,1),(1,e)递减,在(e,+∞)递增,(2)由f′(x)= ![]() ﹣a≤0在(1,+∞)上恒成立,得x∈(1,+∞)时,f′(x)max≤0,从而f′(x)=﹣
﹣a≤0在(1,+∞)上恒成立,得x∈(1,+∞)时,f′(x)max≤0,从而f′(x)=﹣ ![]() +
+ ![]() ﹣a,故当
﹣a,故当 ![]() =
= ![]() ,即x=e2时,f′(x)max=
,即x=e2时,f′(x)max= ![]() ﹣a,得
﹣a,得 ![]() ﹣a≤0,于是a≥
﹣a≤0,于是a≥ ![]() ,故a的最小值为
,故a的最小值为 ![]() .
.
【考点精析】本题主要考查了函数单调性的性质和利用导数研究函数的单调性的相关知识点,需要掌握函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集;一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能正确解答此题.
在这个区间单调递减才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面ABCD是菱 形,PA=PB,且侧面PAB⊥平面ABCD,点E是AB的中点.
中,底面ABCD是菱 形,PA=PB,且侧面PAB⊥平面ABCD,点E是AB的中点.
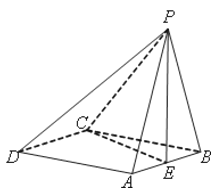
(1)求证:PE⊥AD;
(2)若CA=CB,求证:平面PEC⊥平面PAB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() =
=![]() =
= ![]() .
.
(1)求函数![]() 的单调递增区间;(只需写出结论即可)
的单调递增区间;(只需写出结论即可)
(2)设函数![]() =
= ![]() ,若
,若![]() 在区间
在区间![]() 上有两个不同的零点,求实数
上有两个不同的零点,求实数![]() 的取值范围;
的取值范围;
(3)若存在实数![]() ,使得对于任意的
,使得对于任意的![]() ,都有
,都有![]() 成立,求实数
成立,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线l的参数方程为  (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ=4cosθ.
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ=4cosθ.
(1)把曲线C的极坐标方程化为直角坐标方程;
(2)设直线l与曲线C交于M,N两点,点A(1,0),求 ![]() +
+ ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
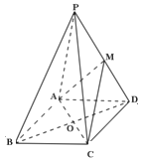
【题目】如图,已知在正四棱锥![]() 中,
中, ![]() 为侧棱
为侧棱![]() 的中点, 连接
的中点, 连接![]() 相交于点
相交于点![]() 。
。
(1)证明: ![]() ;
;
(2)证明: ![]() ;
;
(3)设![]() ,若质点从点
,若质点从点![]() 沿平面
沿平面![]() 与平面
与平面![]() 的表 面运动到点
的表 面运动到点![]() 的最短路径恰好经过点
的最短路径恰好经过点![]() ,求正四棱锥
,求正四棱锥 ![]() 的体积。
的体积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com