
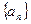 满足
满足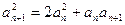 ,且
,且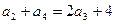 ,其中
,其中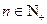 .
.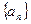 的通项公式;
的通项公式;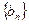 的前
的前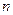 项和为
项和为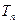 ,令
,令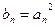 ,其中
,其中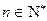 ,试比较
,试比较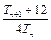 与
与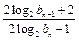 的大小,并加以证明.
的大小,并加以证明.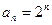
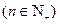
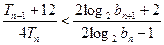
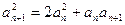 ,即
,即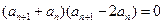 ………2分
………2分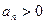 ,所以有
,所以有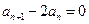 ,所以
,所以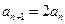 …………3分
…………3分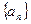 是公比为
是公比为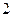 的等比数列,由
的等比数列,由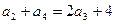 得
得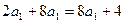 ,解得
,解得 ……4分
……4分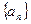 的通项公式为
的通项公式为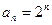
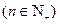 …………5分
…………5分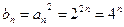 ,………6分,所以
,………6分,所以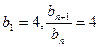
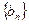 是首项为
是首项为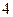 ,公比是
,公比是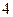 的等比数列,所以
的等比数列,所以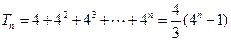 …………7分
…………7分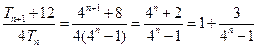 ,又
,又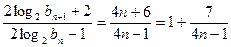
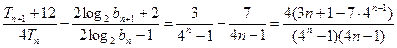 ………9分
………9分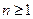 时,
时,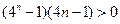
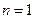 时,
时,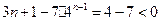 ,当
,当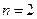 时,
时,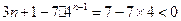
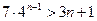 (
(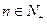 )…………10分,下面用数学归纳法证明
)…………10分,下面用数学归纳法证明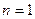 时,
时,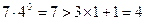 ,上面不等式显然成立;………11分
,上面不等式显然成立;………11分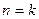 时,不等式
时,不等式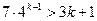 成立…………12分
成立…………12分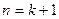 时,
时,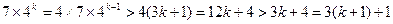 ………13分
………13分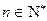 均有
均有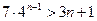
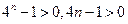 ,所以对任意的
,所以对任意的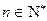 均有
均有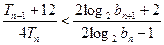 …………14分
…………14分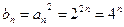 ,………6分,所以
,………6分,所以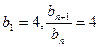
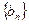 是首项为
是首项为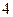 ,公比是
,公比是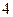 的等比数列,所以
的等比数列,所以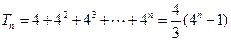 …………7分
…………7分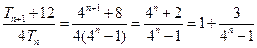 ,又
,又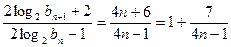
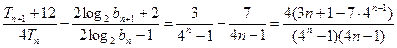 ………9分
………9分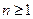 时,
时,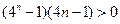 ………10分
………10分 ………12分
………12分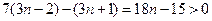 ,∴
,∴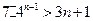 ………13分
………13分 ,即对任意的
,即对任意的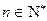 均有
均有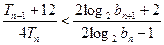 ………14分
………14分

 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:高中数学 来源:不详 题型:解答题
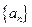 是以4为首项的正数数列,双曲线
是以4为首项的正数数列,双曲线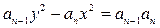 的一个焦点坐标为
的一个焦点坐标为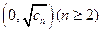 , 且
, 且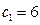 , 一条渐近线方程为
, 一条渐近线方程为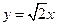 .
.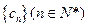 的通项公式;
的通项公式;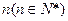 ,不等式
,不等式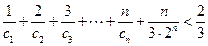 是否恒成立?并说明理由.
是否恒成立?并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com