
分析 (1)根据半焦距c=$\sqrt{13}$,设椭圆长半轴为a,由离心率之比求出a,进而求出椭圆短半轴的长及双曲线的虚半轴的长,写出椭圆和双曲线的标准方程;
(2)由椭圆、双曲线的定义求出PF1与PF2的长,在三角形F1PF2中,利用余弦定理求出 cos∠F1PF2 的值,进一步求得sin∠F1PF2 的值,代入面积公式得答案.
解答 解:(1)由题意知,半焦距c=$\sqrt{13}$,设椭圆长半轴为a,则双曲线实半轴a-4,
离心率之比为$\frac{3}{7}$=$\frac{\frac{\sqrt{13}}{a}}{\frac{\sqrt{13}}{a-4}}$,解得a=7,
∴椭圆的短半轴长等于$\sqrt{49-13}=6$,
双曲线虚半轴的长为$\sqrt{13-9}=2$,
∴椭圆和双曲线的方程分别为:$\frac{{x}^{2}}{49}+\frac{{y}^{2}}{36}=1$和$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{4}=1$;
(2)由椭圆的定义得:PF1 +PF2=2a=14,
由双曲线的定义得:PF1-PF2=6,
∴PF1=10,PF2=4,
又F1F2=2$\sqrt{13}$,在三角形F1PF2中,利用余弦定理得:$(2\sqrt{13})^{2}$=100+16-80cos∠F1PF2,
∴cos∠F1PF2=$\frac{4}{5}$,则sin$∠{F}_{1}P{F}_{2}=\frac{3}{5}$.
∴${S}_{△{F}_{1}P{F}_{2}}$=$\frac{1}{2}P{F}_{1}•P{F}_{2}•sin∠{F}_{1}P{F}_{2}$=$\frac{1}{2}×10×4×\frac{3}{5}=12$.
点评 本题主要考查椭圆、双曲线的标准方程和几何性质、平面向量数量积的运算,考查计算能力,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{17\sqrt{17}}{6}π$ | B. | 17π | C. | $\frac{17π}{2}$ | D. | $\frac{17π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届湖南衡阳八中高三上学期月考二数学(理)试卷(解析版) 题型:解答题
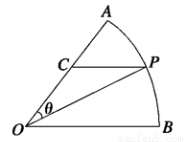
公园里有一扇形湖面,管理部门打算在湖中建一三角形观景平台,希望面积与周长都最大.如图所示扇形 ,圆心角
,圆心角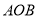 的大小等于
的大小等于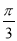 ,半径为
,半径为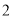 百米,在半径
百米,在半径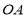 上取一点
上取一点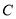 ,过点
,过点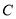 作平行于
作平行于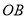 的直线交弧
的直线交弧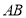 于点
于点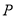 .设
.设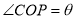 .
.
(1)求△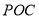 面积
面积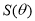 的函数表达式.
的函数表达式.
(2)求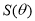 的最大值及此时
的最大值及此时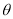 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com