
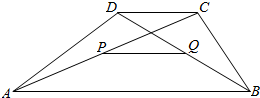
 设P,Q分别是梯形ABCD的对角线AC与BD的中点
设P,Q分别是梯形ABCD的对角线AC与BD的中点分析 (1)用向量表示$\overrightarrow{CQ}$,$\overrightarrow{CP}$,得出向量$\overrightarrow{PQ}$与$\overrightarrow{AB}$、$\overrightarrow{CD}$的关系,再根据向量$\overrightarrow{CD}$与$\overrightarrow{AB}$共线,得出向量$\overrightarrow{AB}$与$\overrightarrow{PQ}$共线即可;
(2)根据向量$\overrightarrow{AB}$与$\overrightarrow{CD}$反向,且|$\overrightarrow{AB}$|=3|$\overrightarrow{CD}$|得出向量$\overrightarrow{PQ}$与$\overrightarrow{AB}$的数量关系,即得PQ:AB的值.
解答 解:(1)∵Q为BD中点,∴$\overrightarrow{CB}$+$\overrightarrow{CD}$=2$\overrightarrow{CQ}$,
又 P为AC中点,∴$\overrightarrow{CA}$=2$\overrightarrow{CP}$;
∴2$\overrightarrow{PQ}$=2$\overrightarrow{CQ}$-2$\overrightarrow{CP}$=($\overrightarrow{CB}$+$\overrightarrow{CD}$)-$\overrightarrow{CA}$=$\overrightarrow{CB}$+$\overrightarrow{CD}$+$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{CD}$,
又向量$\overrightarrow{CD}$与$\overrightarrow{AB}$共线,
设向量$\overrightarrow{CD}$=λ$\overrightarrow{AB}$,
则2$\overrightarrow{PQ}$=(1+λ)$\overrightarrow{AB}$,
∴$\overrightarrow{PQ}$=$\frac{1+λ}{2}$$\overrightarrow{AB}$①,
又梯形ABCD中|$\overrightarrow{AB}$|≠|$\overrightarrow{CD}$|,∴λ≠-1,
∴$\overrightarrow{PQ}$∥$\overrightarrow{AB}$,即PQ∥AB;
(2)∵向量$\overrightarrow{AB}$与$\overrightarrow{CD}$反向,且|$\overrightarrow{AB}$|=3|$\overrightarrow{CD}$|;
所以$\overrightarrow{AB}$=-3$\overrightarrow{CD}$,即λ=-$\frac{1}{3}$代入①式,
得$\overrightarrow{PQ}$=$\frac{1-\frac{1}{3}}{2}$$\overrightarrow{AB}$=$\frac{1}{3}$$\overrightarrow{AB}$,
∴PQ:AB=$\frac{1}{3}$.
点评 本题考查了平面向量的线性运算的应用问题,也考查了用向量法证明线线平行的应用问题,是综合性题目.


科目:高中数学 来源: 题型:选择题
| A. | y=x|x| | B. | y=x2,x∈[-1,1] | ||
| C. | $y=-\frac{1}{x},x∈[{-1,0})∪({0,1})$ | D. | y=x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届湖南衡阳八中高三上学期月考二数学(理)试卷(解析版) 题型:填空题
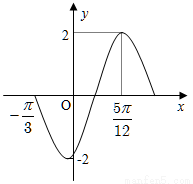
函数f(x)=2sin(ωx+φ)(ω>0,-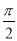 <φ<
<φ<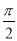 )的部分图象如图所示,则
)的部分图象如图所示,则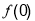 的值是 .
的值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com