Question

【题目】如图在四面体OABC中，OA，OB，OC两两垂直，且OB=OC=3，OA=4，给出如下判断： ①存在点D（O点除外），使得四面体DABC有三个面是直角三角形；
②存在点D，使得点O在四面体DABC外接球的球面上；
③存在唯一的点D使得OD⊥平面ABC；
④存在点D，使得四面体DABC是正棱锥；
⑤存在无数个点D，使得AD与BC垂直且相等．
其中正确命题的序号是（把你认为正确命题的序号填上）．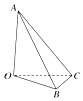

Answer 1

【答案】①②④⑤
【解析】解：对于①，取D为长方体的一个顶点，使得A，B，C是与D相邻的三个顶点，则可使四面体ABCD有3个面是直角三角形，故正确； 对于②，∵二面角C﹣OA﹣B为直二面角，∴∠BOC=Rt∠，再取同①的点D，使得点O与D为相对的两个长方体的顶点，则点O在四面体ABCD的外接球球面上，故正确；
对于③，过O可以作一条直线与面ABC垂直，点D可以是该直线上任意点，故错
④作△CBD为正三角形，使得AD=DB，则点D使四面体ABCD是正三棱锥，故正确．
⑤过点A作BC的垂面，垂面内过AD的每一条都垂直BC，故正确；
所以答案是：①②④⑤
【考点精析】根据题目的已知条件，利用空间中直线与平面之间的位置关系的相关知识可以得到问题的答案，需要掌握直线在平面内—有无数个公共点；直线与平面相交—有且只有一个公共点；直线在平面平行—没有公共点．