
分析 由g(x)-f(x)=x2-8+2|x|≥0得|x|≥2,从而可得F(x)=$\left\{\begin{array}{l}{{x}^{2}+1,|x|≤2}\\{9-2|x|,|x|>2}\end{array}\right.$,即可求出函数y=F(x)的最大值.
解答 解:由g(x)-f(x)=x2-8+2|x|≥0得|x|≥2;
故F(x)=$\left\{\begin{array}{l}{{x}^{2}+1,|x|≤2}\\{9-2|x|,|x|>2}\end{array}\right.$,
故|x|=2时,有最大值5.
故答案为:5.
点评 本题考查了分段函数,考查学生的计算能力,属于中档题.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{-2+i}{5}$ | B. | $\frac{-2-i}{5}$ | C. | $\frac{2-i}{5}$ | D. | $\frac{2+i}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
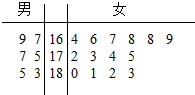 某航空公司在2015年年初招收了20名空乘人员(服务员与空警),其中“男性空乘人员”6名,“女性空乘人员”14名,并对他们的身高进行了测量,其身高(单位:cm)的茎叶图如图所示.公司决定:身高在170以上(包含170cm)的进入“国际航班”做空乘人员,身高在170cm以下的进入“国内航班”做空乘人员.
某航空公司在2015年年初招收了20名空乘人员(服务员与空警),其中“男性空乘人员”6名,“女性空乘人员”14名,并对他们的身高进行了测量,其身高(单位:cm)的茎叶图如图所示.公司决定:身高在170以上(包含170cm)的进入“国际航班”做空乘人员,身高在170cm以下的进入“国内航班”做空乘人员.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com