练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】(2015·上海）设z1, z2C, ，则“z1, z2中至少有一个数是虚数”是“z1-z2是虚数”的（ ）
    A.充分非必要条件
    B.必要非充分条件
    C.充要条件
    D.既非充分又非必要条件

    【答案】B
    【解析】若z1, z2皆是实数，则z1-z2一定不是虚数，因此当z1-z2是虚数时，则“z1, z2中至少有一个数是虚数”成立，即必要性成立; 当z1, z2中至少有一个数是虚数，z1-z2不一定是虚数，如z1=z2=i，即充分性不成立，选B.
    形如a+bi(a,b ∈ R)的数叫复数，其中a，b分别是它的实部和虚部.若b=0，则a+bi为实数，若b≠0。，则a+bi为虚数，若a=0且b≠0，则a+bi为纯虚数.判断概念必须从其定义出发，不可想当然.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=f'（1）ex﹣1﹣f（0）x+ 的导数，e为自然对数的底数）g（x）= +ax+b（a∈R，b∈R）
    （Ⅰ）求f（x）的解析式及极值；
    （Ⅱ）若f（x）≥g（x），求 的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C1 ， 抛物线C2焦点均在x轴上，C1的中心和C2顶点均为原点O，从每条曲线上各取两个点，将其坐标记录于表中，则C1的左焦点到C2的准线之间的距离为（ ）

    x

    3

    ﹣2

    4

    y

    -2

    0

    ﹣4


    A. -1
    B. -1
    C.1
    D.2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，我海监船在D岛海域例行维权巡航，某时刻航行至A处，此时测得其北偏东30°方向与它相距20海里的B处有一外国船只，且D岛位于海监船正东18海里处．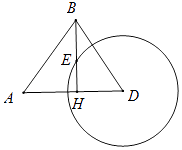
    （1）求此时该外国船只与D岛的距离；
    （2）观测中发现，此外国船只正以每小时4海里的速度沿正南方航行．为了将该船拦截在离D岛12海里的E处（E在B的正南方向），不让其进入D岛12海里内的海域，试确定海监船的航向，并求其速度的最小值（角度精确到0.1°，速度精确到0.1海里/小时）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在正三棱柱ABC﹣A1B1C1中，AB=1，BB1=2，求：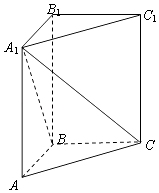
    （1）异面直线B1C1与A1C所成角的大小；
    （2）四棱锥A1﹣B1BCC1的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】用数学归纳法证明12+22+…+（n﹣1）2+n2+（n﹣1）2+…+22+12═ 时，由n=k的假设到证明n=k+1时，等式左边应添加的式子是（ ）
    A.（k+1）2+2k2
    B.（k+1）2+k2
    C.（k+1）2
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】(2015·新课标1卷）执行右面的程序框图，如果输入的t=0.01，则输出的n=（ ）

    A.5
    B.6
    C.10
    D.12

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】[选修4-4：坐标系与参数方程选讲]在平面直角坐标系xOy中，以原点O为极点，x轴的非负半轴为极轴，建立极坐标系，曲线C1的参数方程为 为参数），曲线C2的极坐标方程为 ．
    （1）求曲线C1的普通方程和曲线C2的直角坐标方程；
    （2）设P为曲线C1上一点，Q曲线C2上一点，求|PQ|的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆 的左、右焦点分别为F1 ， F2 ， 上顶点为B，若△BF1F2的周长为6，且点F1到直线BF2的距离为b． （Ⅰ）求椭圆C的方程；
    （Ⅱ）设A1 ， A2是椭圆C长轴的两个端点，点P是椭圆C上不同于A1 ， A2的任意一点，直线A1P交直线x=m于点M，若以MP为直径的圆过点A2 ， 求实数m的值．

    查看答案和解析>>

    同步练习册答案