
分析 由f(x)-f(x-5)=0可判断出函数的周期性,由x∈(-1,4]时函数的解析式,可以求出一个周期内函数的零点个数,进而可得函数f(x)在[0,2016]上的零点个数.
解答 解:∵f(x)-f(x-5)=0,
∴f(x)=f(x-5),
∴f(x)是以5为周期的周期函数,
又∵f(x)=x2-2x在x∈(-1,4]区间内有3个零点,
∴f(x)在任意周期上都有3个零点,
∵x∈(1,2016]上包含403个周期,
又∵x∈[0,1]时不存在零点,
故零点数为3×403=1209.
故答案为:1209.
点评 本题考查的知识点是根的存在性及根的个数判断,其中根据已知分析出函数的周期性是解答的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
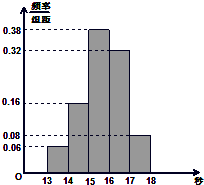 某学校1800名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),第五组[17,18],图是按上述分组方法得到的频率分布直方图.
某学校1800名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),第五组[17,18],图是按上述分组方法得到的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{500}{3}π$ | B. | $\frac{125}{6}π$ | C. | 100π | D. | 25π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com