
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() 为
为![]() 上一点.
上一点.
(1)若![]() 平面
平面![]() ,试说明点
,试说明点![]() 的位置并证明的结论;
的位置并证明的结论;
(2)若![]() 为
为![]() 的中点,
的中点,![]() 平面
平面![]() ,且
,且![]() ,
,
求二面角![]() 的余弦值.
的余弦值.
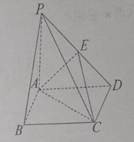
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)当点![]() 为
为![]() 中点时有
中点时有![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,由
,由![]() 为菱形得
为菱形得![]() 是
是![]() 的中点,由三角形的中位线性质可得
的中点,由三角形的中位线性质可得![]() ,即可证明
,即可证明![]() ;(2)以
;(2)以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 为
为![]() 轴和
轴和![]() 轴建立空间直角坐标系,分别求得平面
轴建立空间直角坐标系,分别求得平面![]() 的法向量与平面
的法向量与平面![]() 的法向量,结合图形得二面角
的法向量,结合图形得二面角![]() 为锐二面角,即可求得二面角
为锐二面角,即可求得二面角![]() 的余弦值.
的余弦值.
试题解析:(1)当点![]() 为
为![]() 中点时有
中点时有![]() ,证明如下:
,证明如下:
连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
由菱形性质知点![]() 是
是![]() 的中点.
的中点.
∴![]()
又∵![]()
∴![]() .
.
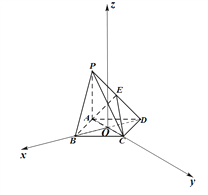
(2)由题意,以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 为
为![]() 轴和
轴和![]() 轴建立如图所示的空间直角坐标系,设
轴建立如图所示的空间直角坐标系,设![]() ,则由条件易知
,则由条件易知![]() ,所以,
,所以,![]() .
.
∴![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则![]() .
.
∴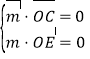 ,即
,即![]() ,令
,令![]() ,则
,则![]() ,所以,
,所以,![]()
同理可求平面![]() 的法向量
的法向量![]() .
.
所以,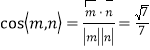 .
.
由图可知,二面角![]() 为锐二面角,故其余弦值为
为锐二面角,故其余弦值为![]()


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:
【题目】下列说法:
①集合{x∈N|x3=x}用列举法表示为{-1,0,1};
②实数集可以表示为{x|x为所有实数}或{R};
③方程组![]() 的解集为{x=1,y=2}.
的解集为{x=1,y=2}.
其中正确的有( )
A.3个B.2个
C.1个D.0个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价 | 4 | 6 | 7 | 8 | 10 |
销量 | 60 | 50 | 45 | 30 | 20 |
(1) 请根据上表提供的数据画出散点图,并判断是正相关还是负相关;
(2) 求出![]() 关于
关于![]() 的回归直线方程,若单价为9元时,预测其销量为多少?
的回归直线方程,若单价为9元时,预测其销量为多少?
(参考公式:回归直线方程中公式 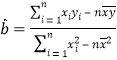 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() .将四边形
.将四边形![]() 沿对角线
沿对角线![]() 折成四面体
折成四面体![]() ,使平面
,使平面![]() 平面
平面![]() ,则下列结论中正确的结论个数是( )
,则下列结论中正确的结论个数是( )


①![]() ;②
;②![]() ;
;
③![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ;
;
④四面体![]() 的体积为
的体积为![]() .
.
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表数据为某地区某种农产品的年产量x(单位:吨)及对应销售价格y(单位:千元/吨) .
x | 1 | 2 | 3 | 4 | 5 |
y | 70 | 65 | 55 | 38 | 22 |
(1)若y与x有较强的线性相关关系,根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程.
(2)若该农产品每吨的成本为13.1千元,假设该农产品可全部卖出,利用上问所求的回归方程,预测当年产量为多少吨时,年利润Z最大?
(参考公式:回归直线方程为![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
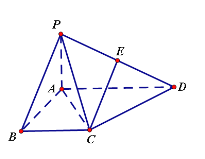
【题目】如图,四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)在棱![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() //平面
//平面![]() ?若存在,请确定
?若存在,请确定![]() 点的位置;若不存在,请说明理由.
点的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 过椭圆
过椭圆![]() 的右焦点
的右焦点![]() ,抛物线
,抛物线![]() 的焦点为椭圆
的焦点为椭圆![]() 的上顶点,且
的上顶点,且![]() 交椭圆
交椭圆![]() 于
于![]() 两点,点
两点,点![]() 在直线
在直线![]() 上的射影依次为
上的射影依次为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 交
交![]() 轴于点
轴于点![]() ,且
,且![]() ,当
,当![]() 变化时,证明:
变化时,证明: ![]() 为定值;
为定值;
(3)当![]() 变化时,直线
变化时,直线![]() 与
与![]() 是否相交于定点?若是,请求出定点的坐标,并给予证明;否则,说明理由.
是否相交于定点?若是,请求出定点的坐标,并给予证明;否则,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能生产A类产品8件和B类产品15件,乙种设备每天能生产A类产品10件和B类产品25件,已知设备甲每天的租赁费300元,设备乙每天的租赁费400元,现车间至少要生产A类产品100件,B类产品200件,所需租赁费最少为__元![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com