
【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价 | 4 | 6 | 7 | 8 | 10 |
销量 | 60 | 50 | 45 | 30 | 20 |
(1) 请根据上表提供的数据画出散点图,并判断是正相关还是负相关;
(2) 求出![]() 关于
关于![]() 的回归直线方程,若单价为9元时,预测其销量为多少?
的回归直线方程,若单价为9元时,预测其销量为多少?
(参考公式:回归直线方程中公式 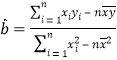 ,
,![]() )
)
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:高中数学 来源: 题型:
【题目】如图,多面体![]() ,
, ![]() ,
,![]()
![]() ,且
,且![]() 两两垂直.给出下列四个命题:
两两垂直.给出下列四个命题:

①三棱锥![]() 的体积为定值;
的体积为定值;
②经过![]() 四点的球的直径为
四点的球的直径为![]() ;
;
③直线![]() ∥平面
∥平面![]() ;
;
④直线![]() 所成的角为
所成的角为![]() ;
;
其中真命题的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若对任意的正整数![]() ,总存在正整数
,总存在正整数![]() ,使得数列
,使得数列![]() 的前
的前![]() 项和
项和![]() ,则称
,则称![]() 是“回归数列”.
是“回归数列”.
(![]() )①前
)①前![]() 项和为
项和为![]() 的数列
的数列![]() 是否是“回归数列”?并请说明理由.②通项公式为
是否是“回归数列”?并请说明理由.②通项公式为![]() 的数列
的数列![]() 是否是“回归数列”?并请说明理由;
是否是“回归数列”?并请说明理由;
(![]() )设
)设![]() 是等差数列,首项
是等差数列,首项![]() ,公差
,公差![]() ,若
,若![]() 是“回归数列”,求
是“回归数列”,求![]() 的值.
的值.
(![]() )是否对任意的等差数列
)是否对任意的等差数列![]() ,总存在两个“回归数列”
,总存在两个“回归数列”![]() 和
和![]() ,使得
,使得![]() 成立,请给出你的结论,并说明理由.
成立,请给出你的结论,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生产企业对其所生产的甲、乙两种产品进行质量检测,分别各抽查6件产品,检测其重量的误差,测得数据如下(单位:![]() ):
):
甲:13 15 13 8 14 21
乙:15 13 9 8 16 23
(1)画出样本数据的茎叶图;
(2)分别计算甲、乙两组数据的方差并分析甲、乙两种产品的质量(精确到0.1)。
查看答案和解析>>
科目:高中数学 来源: 题型:
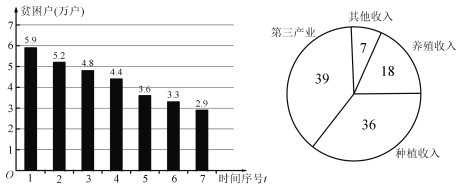
【题目】党的十八大以来,我国精准扶贫已经实施了六年,我国贫困人口从2012年的9899万人,减少到2018年的1660万人,2019年将努力实现减少贫困人口1000万人以上的目标,力争2020年在现行标准下,农村贫困人口全部脱贫,贫困县全部脱贫摘帽.某市为深入分析该市当前扶贫领域存在的突出问题,市扶贫办近三年来,每半年对贫困户(用![]() 表示,单位:万户)进行取样,统计结果如图所示,从2016年6月底到2019年6月底的共进行了七次统计,统计时间用序号
表示,单位:万户)进行取样,统计结果如图所示,从2016年6月底到2019年6月底的共进行了七次统计,统计时间用序号![]() 表示,例如:2016年12月底(时间序号为2)贫困户为5.2万户.
表示,例如:2016年12月底(时间序号为2)贫困户为5.2万户.
(1)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测到2020年12月底,该市能否实现贫困户全部脱贫;
,并预测到2020年12月底,该市能否实现贫困户全部脱贫;
(2)为尽快打赢脱贫攻坚战,该市扶贫办在2019年6月底时,对全市贫困户随机抽取了100户贫困户,对每个家庭最主要经济收入来源进行抽样调查,统计结果如图.并决定据此选派一批农业技术人员对全市所有贫困户中,家庭最主要经济收入来源为养殖收入和种植收入的贫困户进行对口帮扶,每一名农业技术人员对口帮扶贫困户90户,则该市应分别安排多少农业技术人员对家庭最主要经济收入来源为养殖收入和种植收入的贫困户进行对口帮扶?
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
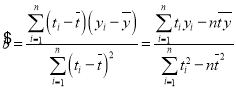 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() :
:![]() ,
,![]() :
:![]() ,则下面结论正确的是( )
,则下面结论正确的是( )
A.把![]() 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移
上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
B.把![]() 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移
上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
C.把![]() 上各点的横坐标缩短到原来的
上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
D.把![]() 上各点的横坐标缩短到原来的
上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高三理科班共有60名同学参加某次考试,从中随机挑选出5名同学,他们的数学成绩![]() 与物理成绩
与物理成绩![]() 如下表:
如下表:

数据表明![]() 与
与![]() 之间有较强的线性关系.
之间有较强的线性关系.
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)该班一名同学的数学成绩为110分,利用(1)中的回归方程,估计该同学的物理成绩;
(3)本次考试中,规定数学成绩达到125分为优秀,物理成绩达到100分为优秀.若该班数学优秀率与物理优秀率分别为![]() 和
和![]() ,且除去抽走的5名同学外,剩下的同学中数学优秀但物理不优秀的同学共有5人.能否在犯错误概率不超过0.01的前提下认为数学优秀与物理优秀有关?
,且除去抽走的5名同学外,剩下的同学中数学优秀但物理不优秀的同学共有5人.能否在犯错误概率不超过0.01的前提下认为数学优秀与物理优秀有关?
参考数据:回归直线的系数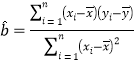 ,
,![]() .
.
![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com