
【题目】如图1,![]() 为等边三角形,
为等边三角形,![]() 分别为
分别为![]() 的中点,
的中点,![]() 为
为![]() 的中点,
的中点,![]() ,将
,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,
,![]()
为![]() 的中点,如图2.
的中点,如图2.

(1)求证:![]() 平面
平面![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
科目:高中数学 来源: 题型:
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:千元)对年销售量
(单位:千元)对年销售量![]() (单位:
(单位:![]() )和年利润
)和年利润![]() (单位:千元)的影响,对近8年的宣传费
(单位:千元)的影响,对近8年的宣传费![]() 和年销售量
和年销售量![]() 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.

|
|
|
|
|
|
|
46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
表中![]() ,
,![]()
附:对于一组数据![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
(1)根据散点图判断,![]() 与
与![]() ,哪一个适宜作为年销售量
,哪一个适宜作为年销售量![]() 关于年宣传费
关于年宣传费![]() 的回归方程类型(给出判断即可,不必说明理由);
的回归方程类型(给出判断即可,不必说明理由);
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)已知这种产品的年利润![]() 与
与![]() 的关系为
的关系为![]() ,根据(2)的结果回答:当年宣传费
,根据(2)的结果回答:当年宣传费![]() 时,年销售量及年利润的预报值是多少?
时,年销售量及年利润的预报值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数 被称为狄利克雷函数,其中
被称为狄利克雷函数,其中![]() 为实数集,
为实数集,![]() 为有理数集,则关于函数
为有理数集,则关于函数![]() 有如下四个命题:①
有如下四个命题:①![]() ;②函数
;②函数![]() 是偶函数;③任取一个不为零的有理数
是偶函数;③任取一个不为零的有理数![]() ,
,![]() 对任意的
对任意的![]() 恒成立;④存在三个点
恒成立;④存在三个点![]() ,
,![]() ,
,![]() ,使得
,使得![]() 为等边三角形.其中真命题的个数有( )
为等边三角形.其中真命题的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() ,侧面
,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上.
上.
(Ⅰ)求证:![]() 平面
平面![]() .
.
(Ⅱ)若![]() 为
为![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() .
.
(Ⅲ)如果直线![]() 与平面
与平面![]() 所成的角和直线
所成的角和直线![]() 与平面
与平面![]() 所在的角相等,求
所在的角相等,求![]() 的值.
的值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种计算机病毒是通过电子邮件进行传播的,下表是某公司前5天监测到的数据:
第 | 1 | 2 | 3 | 4 | 5 |
被感染的计算机数量 | 10 | 20 | 39 | 81 | 160 |
则下列函数模型中,能较好地反映计算机在第![]() 天被感染的数量
天被感染的数量![]() 与
与![]() 之间的关系的是
之间的关系的是
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)=Acos(ωx+φ)+B的部分图象如图所示,将函数g(x)的图象保持纵坐标不变,横坐标向右平移![]() 个单位长度后得到函数f(x)的图象.求:
个单位长度后得到函数f(x)的图象.求:
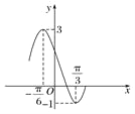
(1)函数f(x)在![]() 上的值域;
上的值域;
(2)使f(x)≥2成立的x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲同学参加化学竞赛初赛,考试分为笔试、口试、实验三个项目,各单项通过考试的概率依次为![]() 、
、![]() 、
、![]() ,笔试、口试、实验通过考试分别记4分、2分、4分,没通过的项目记0分,各项成绩互不影响.
,笔试、口试、实验通过考试分别记4分、2分、4分,没通过的项目记0分,各项成绩互不影响.
(Ⅰ)若规定总分不低于8分即可进入复赛,求甲同学进入复赛的概率;
(Ⅱ)记三个项目中通过考试的个数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com