
【题目】大学先修课程,是在高中开设的具有大学水平的课程,旨在让学有余力的高中生早接受大学思维方式、学习方法的训练,为大学学习乃至未来的职业生涯做好准备.某高中成功开设大学先修课程已有两年,共有250人参与学习先修课程.
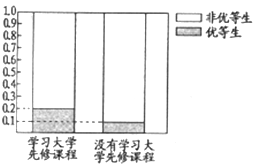
(Ⅰ)这两年学校共培养出优等生150人,根据下图等高条形图,填写相应列联表,并根据列联表检验能否在犯错的概率不超过0.01的前提下认为学习先修课程与优等生有关系?
优等生 | 非优等生 | 总计 | |
学习大学先修课程 | 250 | ||
没有学习大学先修课程 | |||
总计 | 150 |
(Ⅱ)某班有5名优等生,其中有2名参加了大学生先修课程的学习,在这5名优等生中任选3人进行测试,求这3人中至少有1名参加了大学先修课程学习的概率.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式:![]() ,其中
,其中![]()
【答案】(1)列联表见解析 有关系(2)![]()
【解析】
(1)根据优等生的人数、学习大学先修课程的人数,结合等高条形图计算数值,填写好表格,计算出![]() 的值,比较题目所给参考数据,得出“在犯错误的概率不超过0.01的前提下认为学习先修课程与优等生有关系”这个结论.(2)利用列举法,求得基本事件的众数为
的值,比较题目所给参考数据,得出“在犯错误的概率不超过0.01的前提下认为学习先修课程与优等生有关系”这个结论.(2)利用列举法,求得基本事件的众数为![]() 种,其中“没有学生参加大学先修课程学习” 的情况有
种,其中“没有学生参加大学先修课程学习” 的情况有![]() 种,利用对立事件的概率计算方法,求得至少有
种,利用对立事件的概率计算方法,求得至少有![]() 名参加了大学先修课程学习的概率.
名参加了大学先修课程学习的概率.
(1)列联表如下:
优等生 | 非优等生 | 总计 | |
学习大学先修课程 | 50 | 200 | 250 |
没有学习大学先修课程 | 100 | 900 | 1000 |
总计 | 150 | 1100 | 1250 |
由列联表可得![]() ,
,
因此在犯错误的概率不超过0.01的前提下认为学习先修课程与优等生有关系.
(2)在这5名优等生中,记参加了大学先修课程的学习的2名学生为![]() ,
,![]() ,记没有参加大学先修课程学习的3名学生为
,记没有参加大学先修课程学习的3名学生为![]() ,
,![]() ,
,![]() .
.
则所有的抽样情况如下:共10种,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
其中没有学生参加大学先修课程学习的情况有1种,为![]() .
.
记事件![]() 为至少有1名学生参加了大学先修课程的学习,则
为至少有1名学生参加了大学先修课程的学习,则![]() .
.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】对于数列![]() ,若存在常数M>0,对任意的n∈N*,恒有
,若存在常数M>0,对任意的n∈N*,恒有![]() ,则称数列
,则称数列![]() 为B-数列.
为B-数列.
(1)首项为1,公比q(![]() )的等比数列是否为B-数列?请说明理由;
)的等比数列是否为B-数列?请说明理由;
(2)设Sn是数列{xn}的前n项和,给出下列两组论断:
A组:①数列{xn}是B-数列,②数列{xn}不是B-数列
B组:①数列{Sn}是B-数列,②数列{Sn}不是B-数列
请以其中一组的一个论断为条件,另一组的一个论断为结论组成一个命题.判断所给命题的真假,并证明你的结论.
(3)若数列{an}、![]() 都是B-数列,证明:数列{anbn}也是B-数列
都是B-数列,证明:数列{anbn}也是B-数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求![]() 与
与![]() 的交点的直角坐标;
的交点的直角坐标;
(2)求![]() 上的点到直线
上的点到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 与直线
与直线![]() 平行,且过坐标原点,圆
平行,且过坐标原点,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求直线![]() 和圆
和圆![]() 的极坐标方程;
的极坐标方程;
(2)设直线![]() 和圆
和圆![]() 相交于点
相交于点![]() 、
、![]() 两点,求
两点,求![]() 的周长.
的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为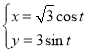 (t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程是
(t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程是![]() ,曲线
,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线l和曲线![]() 的直角坐标方程,曲线
的直角坐标方程,曲线![]() 的普通方程;
的普通方程;
(2)若直线l与曲线![]() 和曲线
和曲线![]() 在第一象限的交点分别为P,Q,求
在第一象限的交点分别为P,Q,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,曲线C的参数方程为![]() (
(![]() 为参数),以平面直角坐标系的原点O为极点,x轴正半轴为极轴建立极坐标系.
为参数),以平面直角坐标系的原点O为极点,x轴正半轴为极轴建立极坐标系.
(1)求曲线C的极坐标方程;
(2)过点![]() ,倾斜角为
,倾斜角为![]() 的直线l与曲线C相交于M,N两点,求
的直线l与曲线C相交于M,N两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班制定了数学学习方案:星期一和星期日分别解决![]() 个数学问题,且从星期二开始,每天所解决问题的个数与前一天相比,要么“多一个”要么“持平”要么“少一个”,则在一周中每天所解决问题个数的不同方案共有( )
个数学问题,且从星期二开始,每天所解决问题的个数与前一天相比,要么“多一个”要么“持平”要么“少一个”,则在一周中每天所解决问题个数的不同方案共有( )
A. ![]() 种 B.
种 B. ![]() 种 C.
种 C. ![]() 种 D.
种 D. ![]() 种
种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com