
分析 (1)通过换元,将函数转化为关于t的二次函数,求出对称轴,通过对对称轴与区间位置关系的讨论,求出最小值h(a);
(2)(Ⅰ)由新定义,假设h(x)为“和谐函数”,讨论p,q的范围,通过方程的解即可判断;
(Ⅱ)据和谐函数的定义,列出方程组,可得p2,q2为方程$\sqrt{x-1}$+t=x的二实根,再由二次方程实根的分布,即可得到所求t的范围.
解答 解:(1)令t=3-x,x∈[-1,1].由(1)知t∈[$\frac{1}{3}$,3].
∴函数y=[f(x)]2-2af(x)+3=t2-2at+3,
对称轴x=a(a≤3)①a≤$\frac{1}{3}$时,ymin=($\frac{1}{3}$)2-$\frac{2}{3}$a+3=$\frac{28}{9}$-$\frac{2}{3}$a,
②$\frac{1}{3}$<a≤3时,ymin=a2-2a2+3=3-a2.
∴h(a)=$\left\{\begin{array}{l}{\frac{28}{9}-\frac{2a}{3},a≤\frac{1}{3}}\\{3-{a}^{2},\frac{1}{3}<a≤3}\end{array}\right.$.
(2)(I)若h(x)为“和谐函数”,
则h(x)在(-∞,3]上存在区间[p,q](p<q),使得g(x)在区间[p,q]
上的值域为[p2,q2].
①若p<q≤$\frac{1}{3}$,h(x)递减,$\left\{\begin{array}{l}{\frac{28}{9}-\frac{2}{3}p={q}^{2}}\\{\frac{28}{9}-\frac{2}{3}q={p}^{2}}\end{array}\right.$,得p+q=$\frac{2}{3}$,
这与p<q≤$\frac{1}{3}$矛盾.
②-3<p<q≤3时$\left\{\begin{array}{l}{3-{p}^{2}={q}^{2}}\\{3-{q}^{2}={p}^{2}}\end{array}\right.$恒成立
此时p、q、满足$\left\{\begin{array}{l}{{p}^{2}+{q}^{2}=3}\\{\frac{1}{3}≤p<q≤3}\end{array}\right.$,这样的p,q存在.
③p<$\frac{1}{3}$,$\frac{1}{3}$<q≤3时,解得p=$\frac{1}{3}$矛盾.
∴(1)中h(x)是“和谐函数”,p、q满足$\left\{\begin{array}{l}{{p}^{2}+{q}^{2}=3}\\{\frac{1}{3}≤p<q≤3}\end{array}\right.$;
(II)∵y=$\sqrt{{x}^{2}-1}$+t在[1,+∞)递增,
由和谐函数的定义知,该函数在定义域[1,+∞)内,
存在区间[p,q](p<q),使得该函数在区间[p,q]上的值域为[p2,q2],所以p≥1,$\left\{\begin{array}{l}{\sqrt{{p}^{2}-1}+t={p}^{2}}\\{\sqrt{{q}^{2}-1}+t={q}^{2}}\end{array}\right.$,
∴p2,q2为方程$\sqrt{x-1}$+t=x的二实根,
即方程x2-(2t+1)x+t2+1=0在[1,+∞)上存在两个不等的实根,
且x≥t恒成立,
令u(x)=x2-(2t+1)x+t2+1,
∴$\left\{\begin{array}{l}{△>0}\\{\frac{2t+1}{2}>1}\\{u(1)≥0}\\{t≤1}\end{array}\right.$,∴$\left\{\begin{array}{l}{t>\frac{3}{4}}\\{t>\frac{1}{2}}\\{(t-1)^{2}≥0}\\{t≤1}\end{array}\right.$,
解得$\frac{3}{4}$<t≤1
∴实数t的取值范围($\frac{3}{4}$,1].
点评 本题考查新定义题,关键是理解题中的新定义,此题型是近几年高考常考题型.求分段函数的函数值关键是判断出自变量所属的范围.


科目:高中数学 来源: 题型:选择题
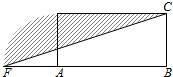 设计一个商标图案如图中阴影部分,矩形ABCD中,AB=2BC,且AB=8cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积等于( )
设计一个商标图案如图中阴影部分,矩形ABCD中,AB=2BC,且AB=8cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积等于( )| A. | (4π+8)cm2 | B. | (4π+16)cm2 | C. | (3π+8)cm2 | D. | (3π+16)cm2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<c<b | B. | a<b<c | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com