
 如图,在△ABC中,AB=BC=2,∠ABC=120°.若平面ABC外的点P和线段AC上的点D,满足PD=DA,PB=BA,则四面体PBCD的体积的最大值是$\frac{1}{2}$.
如图,在△ABC中,AB=BC=2,∠ABC=120°.若平面ABC外的点P和线段AC上的点D,满足PD=DA,PB=BA,则四面体PBCD的体积的最大值是$\frac{1}{2}$. 分析 由题意,△ABD≌△PBD,可以理解为△PBD是由△ABD绕着BD旋转得到的,对于每段固定的AD,底面积BCD为定值,要使得体积最大,△PBD必定垂直于平面ABC,此时高最大,体积也最大.
解答 解:如图,M是AC的中点.
①当AD=t<AM=$\sqrt{3}$时,如图,此时高为P到BD的距离,也就是A到BD的距离,即图中AE,
DM=$\sqrt{3}$-t,由△ADE∽△BDM,可得$\frac{h}{1}=\frac{t}{\sqrt{(\sqrt{3}-t)^{2}+1}}$,∴h=$\frac{t}{\sqrt{(\sqrt{3}-t)^{2}+1}}$,
V=$\frac{1}{3}•\frac{1}{2}•(2\sqrt{3}-t)•1•$$\frac{t}{\sqrt{(\sqrt{3}}-t)^{2}+1}$=$\frac{1}{6}•$$\frac{3-(\sqrt{3}-t)^{2}}{\sqrt{(\sqrt{3}-t)^{2}+1}}$,t∈(0,$\sqrt{3}$)
②当AD=t>AM=$\sqrt{3}$时,如图,此时高为P到BD的距离,也就是A到BD的距离,即图中AH,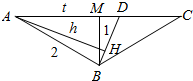
DM=t-$\sqrt{3}$,由等面积,可得$\frac{1}{2}•AD•BM=\frac{1}{2}•BD•AH$,∴$\frac{1}{2}•t•1=\frac{1}{2}\sqrt{(t-\sqrt{3})^{2}+1}$,
∴h=$\frac{t}{\sqrt{(\sqrt{3}-t)^{2}+1}}$,
∴V=$\frac{1}{3}•\frac{1}{2}•(2\sqrt{3}-t)•1•$$\frac{t}{\sqrt{(\sqrt{3}}-t)^{2}+1}$=$\frac{1}{6}•$$\frac{3-(\sqrt{3}-t)^{2}}{\sqrt{(\sqrt{3}-t)^{2}+1}}$,t∈($\sqrt{3}$,2$\sqrt{3}$)
综上所述,V=$\frac{1}{6}•$$\frac{3-(\sqrt{3}-t)^{2}}{\sqrt{(\sqrt{3}-t)^{2}+1}}$,t∈(0,2$\sqrt{3}$)
令m=$\sqrt{(\sqrt{3}-t)^{2}+1}$∈[1,2),则V=$\frac{1}{6}•\frac{4-{m}^{2}}{m}$,∴m=1时,Vmax=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查体积最大值的计算,考查学生转化问题的能力,考查分类讨论的数学思想,对思维能力和解题技巧有一定要求,难度大.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,3] | B. | (-2,3] | C. | [1,2) | D. | (-∞,-2]∪[1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-$\frac{3}{4}$x | B. | y=$\frac{3}{4}$x | C. | y=-$\frac{3}{4}$x或x=0 | D. | y=$\frac{3}{4}$x或x=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
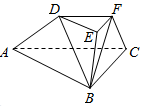 如图,在三棱台ABC-DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.
如图,在三棱台ABC-DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com