
| A. | $\frac{{\sqrt{10}}}{2}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\frac{{\sqrt{7}}}{2}$ | D. | 2 |
分析 判断出E为PF的中点,据双曲线的特点知原点O为两焦点的中点;利用中位线的性质,求出PF′的长度及判断出PF′垂直于PF;通过勾股定理得到a,c的关系,求出双曲线的离心率.
解答  解:∵$\overline{OP}=2\overline{OE}-\overline{OF}$,则$\overrightarrow{OE}=\frac{1}{2}(\overrightarrow{OP}+\overrightarrow{OF})$,∴E为PF的中点,令右焦点为F′,则O为FF′的中点,
解:∵$\overline{OP}=2\overline{OE}-\overline{OF}$,则$\overrightarrow{OE}=\frac{1}{2}(\overrightarrow{OP}+\overrightarrow{OF})$,∴E为PF的中点,令右焦点为F′,则O为FF′的中点,
则PF′=2OE=a,∵E为切点,∴OE⊥PF,
∴PF′⊥PF,∵PF-PF′=2a,∴PF=PF′+2a=3a,
在Rt△PFF′中,PF2+PF′2=FF′2,即9a2+a2=4c2.
所以离心率e=$\frac{c}{a}=\frac{\sqrt{10}}{2}$.
故选:A.
点评 本小题主要考查双曲线的简单性质、圆的方程等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想,在圆锥曲线中,求离心率关键就是求三参数a,b,c的关系,属于中档题


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
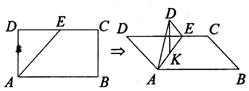 如图在矩形ABCD中,AB=2$\sqrt{3}$,BC=2,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )
如图在矩形ABCD中,AB=2$\sqrt{3}$,BC=2,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{{\sqrt{6}+\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{6}+\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
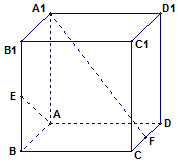 如图,正方体ABCD-A1B1C1D1的棱长为1,E、F分别是BB1和CD的中点.
如图,正方体ABCD-A1B1C1D1的棱长为1,E、F分别是BB1和CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±x | B. | $y=±\frac{{\sqrt{2}}}{2}x$ | C. | $y=±\sqrt{2}x$ | D. | $y=±\frac{1}{2}x$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com