
设函数 ,其中
,其中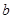 为常数。
为常数。
(Ⅰ)当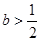 时,判断函数
时,判断函数 在定义域上的单调性;
在定义域上的单调性;
(Ⅱ)若函数 有极值点,求
有极值点,求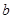 的取值范围及
的取值范围及 的极值点。
的极值点。
(Ⅰ)函数 在定义域
在定义域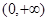 上单调递增;(Ⅱ)当且仅当
上单调递增;(Ⅱ)当且仅当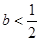 时
时 有极值点; 当
有极值点; 当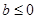 时,
时, 有惟一最小值点
有惟一最小值点 ;当
;当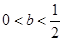 时,
时, 有一个极大值点
有一个极大值点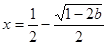 和一个极小值点
和一个极小值点 .
.
解析试题分析:(Ⅰ)函数
科目:高中数学
来源:
题型:解答题
如图所示,将一矩形花坛
科目:高中数学
来源:
题型:解答题
已知
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 在定义域上的单调性的方法,一是利用定义,二是利用导数,此题既有代数函数又有对数函数,显然利用导数判断,只需对
在定义域上的单调性的方法,一是利用定义,二是利用导数,此题既有代数函数又有对数函数,显然利用导数判断,只需对 求导,判断
求导,判断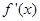 的符号即可;(Ⅱ)求
的符号即可;(Ⅱ)求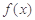 的极值,只需对
的极值,只需对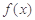 求导即可,利用导数求函数的极值一般分为四个步骤:①确定函数的定义域;②求出
求导即可,利用导数求函数的极值一般分为四个步骤:①确定函数的定义域;②求出 ;③令
;③令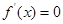 ,列表;④确定函数的极值.此题由(Ⅰ)得,当
,列表;④确定函数的极值.此题由(Ⅰ)得,当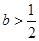 时,函数
时,函数 无极值点,只需讨论
无极值点,只需讨论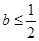 的情况,解
的情况,解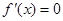 的根,讨论在
的根,讨论在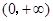 范围内根的个数,从而确定
范围内根的个数,从而确定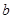 的取值范围及
的取值范围及 的极值点,值得注意的是,求出
的极值点,值得注意的是,求出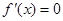 的根时,忽略讨论根是否在定义域内,而出错.
的根时,忽略讨论根是否在定义域内,而出错.
试题解析:(Ⅰ)由题意知, 的定义域为
的定义域为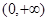 ,
,
 ∴当
∴当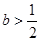 时,
时,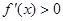 ,函数
,函数 在定义域
在定义域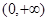 上单调递增.
上单调递增.
(Ⅱ)①由(Ⅰ)得,当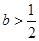 时,函数
时,函数 无极值点,②
无极值点,② 时,
时,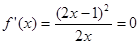 有两个相同的解
有两个相同的解 ,但当
,但当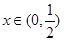 时,
时,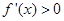 ,当
,当 时,
时,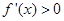
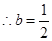 时,函数
时,函数 在
在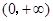 上无极值点,③当
上无极值点,③当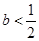 时,
时,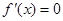 有两个不同解,
有两个不同解,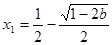
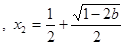 ,
,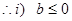 时,
时, ,而
,而 ,此时
,此时 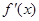 ,
, 随
随 在定义域上的变化情况如下表:
在定义域上的变化情况如下表:
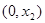
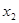
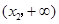
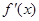


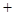

减 

开放课堂义务教育新课程导学案系列答案
二期课改配套教辅读物系列答案
小学单元测试卷系列答案
新课程单元检测新疆电子音像出版社系列答案
赢在新课堂随堂小测系列答案
品学双优赢在期末系列答案
优等生测评卷系列答案

期末红100系列答案
冠军练加考课时作业单元期中期末检测系列答案
 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛 ,要求
,要求 在
在 的延长线上,
的延长线上, 在
在 的延长线上,且对角线
的延长线上,且对角线 过
过 点.已知
点.已知 米,
米, 米。
米。
(1)设 (单位:米),要使花坛
(单位:米),要使花坛 的面积大于32平方米,求
的面积大于32平方米,求 的取值范围;
的取值范围;
(2)若 (单位:米),则当
(单位:米),则当 ,
, 的长度分别是多少时,花坛
的长度分别是多少时,花坛 的面积最大?并求出最大面积.
的面积最大?并求出最大面积. 是实数,函数
是实数,函数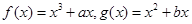 ,
, 和
和 ,分别是
,分别是 的导函数,若
的导函数,若 在区间
在区间 上恒成立,则称
上恒成立,则称 和
和 在区间
在区间 上单调性一致.
上单调性一致.
(Ⅰ)设 ,若函数
,若函数 和
和 在区间
在区间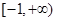 上单调性一致,求实数
上单调性一致,求实数 的取值范围;
的取值范围;
(Ⅱ)设 且
且 ,若函数
,若函数 和
和 在以
在以 为端点的开区间上单调性一致,求
为端点的开区间上单调性一致,求 的最大值.
的最大值.
版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号