
【题目】已知函数![]() ,且
,且![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)在函数![]() 的图象上任意取定两点
的图象上任意取定两点![]() ,
,![]() ,记直线
,记直线![]() 的斜率为
的斜率为![]() ,求证:存在唯一
,求证:存在唯一![]() ,使得
,使得![]() 成立.
成立.
【答案】(Ⅰ)![]() ;(Ⅱ)证明见解析.
;(Ⅱ)证明见解析.
【解析】
(Ⅰ)先对函数求导得![]() ,分类讨论
,分类讨论![]() 和
和![]() ,利用导数研究函数的单调性和极值,结合
,利用导数研究函数的单调性和极值,结合![]() ,结合极值与最值关系可求出
,结合极值与最值关系可求出![]() 的值;
的值;
(Ⅱ)根据题意,由直线的斜率公式并转化后得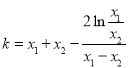 ,构造函数
,构造函数![]() ,并利用导数研究函数
,并利用导数研究函数![]() 的单调性,将证明存在唯一
的单调性,将证明存在唯一![]() ,使得
,使得![]() 成立,转化为证明不等式
成立,转化为证明不等式![]() ,
,![]() 即可,分别求出
即可,分别求出![]() 和
和![]() ,再构造函数并根据导数研究单调性和利用导数证明不等式,即可证出.
,再构造函数并根据导数研究单调性和利用导数证明不等式,即可证出.
解:(Ⅰ)由题可知,![]() ,则
,则![]() 的定义域为
的定义域为![]() ,
,
则![]() ,
,
由于![]() ,
,
当![]() 时,因为
时,因为![]() ,所以不满足题意;
,所以不满足题意;
当![]() 时,令
时,令![]() ,解得
,解得![]() ,
,
当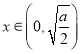 时,
时,![]() ,
,![]() 在区间
在区间![]() 上单调递减,
上单调递减,
当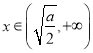 时,
时,![]() ,
,![]() 在区间
在区间![]() 上单调递增,
上单调递增,
故![]() 是
是![]() 在
在![]() 的唯一最小值点,
的唯一最小值点,
由于![]() ,所以当且仅当
,所以当且仅当![]() ,
,
即![]() 时,
时,![]() ,故
,故![]() .
.
(Ⅱ)由题意知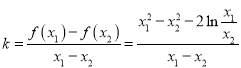
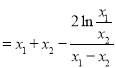 ,
,
令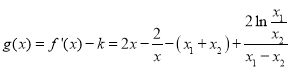 ,
,
则![]() ,故
,故![]() 在区间
在区间![]() 上单调递增,
上单调递增,
故要证:存在唯一![]() ,使得
,使得![]() 成立,
成立,
只需证:![]() ,
,![]() 即可,
即可,
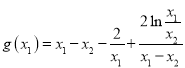
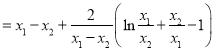 ,
,
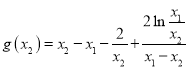
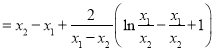 ,
,
令![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在区间
在区间![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() ,
,![]() 在区间
在区间![]() 上单调递减,
上单调递减,
故![]() ,
,
令![]() 时,有
时,有![]() ,
,
又因为![]() ,
,![]() ,因此
,因此![]() ,
,
由![]() ,令
,令![]() ,得
,得![]() ,
,
令![]() 时,有
时,有![]() ,
,
又因为![]() ,因此
,因此![]() ,
,
综上,存在唯一![]() ,使得
,使得![]() 成立.
成立.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() ,底面
,底面![]() 为菱形,
为菱形,![]() ,
,![]() 为
为![]() 上的点,过
上的点,过![]() 的平面分别交
的平面分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,且
,且![]() 平面
平面![]() .
.
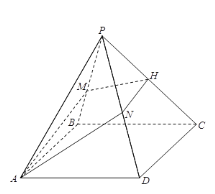
(1)证明:![]() ;
;
(2)当![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某正三棱锥的底面边长为4,侧面与底面所成二面角的余弦值为![]() ,球
,球![]() 为该三棱锥的内切球.球
为该三棱锥的内切球.球![]() 与球
与球![]() 相切,且与该三棱锥的三个侧面也相切,则球
相切,且与该三棱锥的三个侧面也相切,则球![]() 与球
与球![]() 的表面积之比为( )
的表面积之比为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥![]() 中,顶点
中,顶点![]() 在底面
在底面![]() 的投影为
的投影为![]() 的内心,三个侧面的面积分别为12,16,20,且底面面积为24,则三棱锥
的内心,三个侧面的面积分别为12,16,20,且底面面积为24,则三棱锥![]() 的内切球的表面积为( )
的内切球的表面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲、乙两种树苗中各抽测了10株树苗的高度,其茎叶图数据如图.根据茎叶图,下列描述正确的是( )
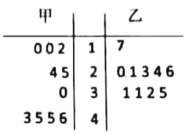
A.甲种树苗的中位数大于乙种树苗的中位数,且甲种树苗比乙种树苗长得整齐
B.甲种树苗的中位数大于乙种树苗的中位数,但乙种树苗比甲种树苗长得整齐
C.乙种树苗的中位数大于甲种树苗的中位数,且乙种树苗比甲种树苗长得整齐
D.乙种树苗的中位数大于甲种树苗的中位数,但甲种树苗比乙种树苗长得整齐
查看答案和解析>>
科目:高中数学 来源: 题型:
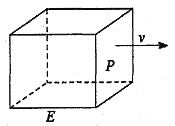
【题目】如图,长方形物体E在雨中沿面P(面积为S)的垂直方向作匀速移动,速度为![]() ,雨速沿E移动方向的分速度为
,雨速沿E移动方向的分速度为![]() 。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与
。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与![]() ×S成正比,比例系数为
×S成正比,比例系数为![]() ;(2)其它面的淋雨量之和,其值为
;(2)其它面的淋雨量之和,其值为![]() ,记
,记![]() 为E移动过程中的总淋雨量,当移动距离d=100,面积S=
为E移动过程中的总淋雨量,当移动距离d=100,面积S=![]() 时。
时。
(1)写出![]() 的表达式
的表达式
(2)设0<v≤10,0<c≤5,试根据c的不同取值范围,确定移动速度![]() ,使总淋雨量
,使总淋雨量![]() 最少。
最少。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年,泉州市区的房价依旧是市民关心的话题.总体来说,二手房房价有所下降;相比二手房而言,新房市场依然强劲,价格持续升高.已知销售人员主要靠售房提成领取工资.现统计泉州市某新房销售人员2019年一年的工资情况的结果如图所示,则下列说法正确的是( )
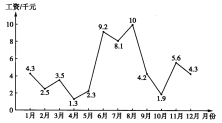
A.2019年该销售人员月工资的中位数为![]()
B.2019年该销售人员8月份的工资增长率最高
C.2019年该销售人员第一季度月工资的方差小于第二季度月工资的方差
D.2019年该销售人员第一季度月工资的平均数大于第四季度月工资的平均数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com