
【题目】已知函数f(x)= ![]() ,其中
,其中 ![]() =(2cosx,
=(2cosx, ![]() sin2x),
sin2x), ![]() =(cosx,1),x∈R
=(cosx,1),x∈R
(1)求函数y=f(x)的最小正周期和单调递增区间:
(2)在△ABC中,角A,B,C所对的边分别为a,b,c,f(A)=2,a= ![]() 且sinB=2sinC,求△ABC的面积.
且sinB=2sinC,求△ABC的面积.
【答案】
(1)解:∵ ![]() =(2cosx,
=(2cosx, ![]() sin2x),
sin2x), ![]() =(cosx,1),x∈R,
=(cosx,1),x∈R,
∴f(x)= ![]() =
= ![]()
= ![]() =2sin(2x+
=2sin(2x+ ![]() )+1,
)+1,
∴函数y=f(x)的最小正周期为T=π,
单调递增区间满足﹣ ![]() +2kπ
+2kπ ![]() +2kπ,k∈Z.
+2kπ,k∈Z.
解得﹣ ![]() +kπ≤x≤
+kπ≤x≤ ![]() +kπ,k∈Z.
+kπ,k∈Z.
∴函数y=f(x)的单调增区间是[﹣ ![]() +kπ,
+kπ, ![]() ],k∈Z.
],k∈Z.
(2)解:∵f(A)=2,∴2sin(2A+ ![]() )+1=2,即sin(2A+
)+1=2,即sin(2A+ ![]() )=
)= ![]() ,
,
又∵0<A<π,∴A= ![]() ,
,
∵ ![]() ,由余弦定理得a2=b2+c2﹣2bccosA=(b+c)2﹣3bc=7,①
,由余弦定理得a2=b2+c2﹣2bccosA=(b+c)2﹣3bc=7,①
∵sinB=2sinC,∴b=2c.②
由①②得c2= ![]() ,∴
,∴ ![]() .
.
【解析】(1)求出f(x)=2sin(2x+ ![]() )+1,由此能求出函数y=f(x)的最小正周期和函数y=f(x)的单调增区间.(2)由f(A)=2,求出A=
)+1,由此能求出函数y=f(x)的最小正周期和函数y=f(x)的单调增区间.(2)由f(A)=2,求出A= ![]() ,由
,由 ![]() ,利用余弦定理得b=2c.由此能求出△ABC的面积.
,利用余弦定理得b=2c.由此能求出△ABC的面积.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 的图象过点(0,﹣1).
的图象过点(0,﹣1).
(1)求实数a的值;
(2)若f(x)=m+ ![]() (m,n是常数),求实数m,n的值;
(m,n是常数),求实数m,n的值;
(3)用定义法证明:函数f(x)在(3,+∞)上是单调减函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且Sn=2n2+n,n∈N* , 数列{bn}满足an=4log2bn+3,n∈N* .
(1)求an , bn;
(2)求数列{anbn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知[x)表示大于x的最小整数,例如[3)=4,[﹣1,3)=﹣1,下列命题中正确的是( ) ①函数f(x)=[x)﹣x的值域是(0,1]
②若{an}是等差数列,则{[an)}也是等差数列
③若{an}是等比数列,则{[an)}也是等比数列
④若x∈(1,2017),则方程[x)﹣x=sin ![]() x有1007个根.
x有1007个根.
A.②
B.③④
C.①
D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在区间
在区间![]() 上有最大值4和最小值1.设
上有最大值4和最小值1.设![]() .
.
(1)求![]() 的值;
的值;
(2)若不等式![]() 在
在![]() 上有解,求实数
上有解,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 有三个不同的实数解,求实数
有三个不同的实数解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[ ![]() ]表示不超过
]表示不超过 ![]() 的最大整数.若 S1=[
的最大整数.若 S1=[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]=3,
]=3,
S2=[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]=10,
]=10,
S3=[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]=21,
]=21,
…,
则Sn=( )
A.n(n+2)
B.n(n+3)
C.(n+1)2﹣1
D.n(2n+1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin( ![]() ﹣x)sinx﹣
﹣x)sinx﹣ ![]() cos2x. (I)求f(x)的最小正周期和最大值;
cos2x. (I)求f(x)的最小正周期和最大值;
(II)讨论f(x)在[ ![]() ,
, ![]() ]上的单调性.
]上的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
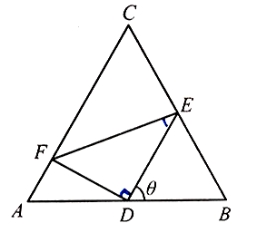
【题目】如图,正三角形ABC的边长为2,D,E,F分别在三边AB,BC和CA上,且D为AB的中点,![]() ,
,![]() ,
,![]() .
.
(1)当![]() 时,求
时,求![]() 的大小;
的大小;
(2)求![]() 的面积S的最小值及使得S取最小值时
的面积S的最小值及使得S取最小值时![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com