
已知函数 ,
, ,且
,且 在点
在点
 处的切线方程为
处的切线方程为 .
.
(1)求 的值;
的值;
(2)若函数 在区间
在区间 内有且仅有一个极值点,求
内有且仅有一个极值点,求 的取值范围;
的取值范围;
(3)设 为两曲线
为两曲线 ,
, 的交点,且两曲线在交点
的交点,且两曲线在交点 处的切线分别为
处的切线分别为 .若取
.若取 ,试判断当直线
,试判断当直线 与
与 轴围成等腰三角形时
轴围成等腰三角形时 值的个数并说明理由.
值的个数并说明理由.
(1) ;(2)
;(2) ;(3)2个
;(3)2个
【解析】
试题分析:(1)由函数 ,在点
,在点 处的切线方程为
处的切线方程为 .所以对函数求导,根据斜率为1以及过点(1,0)两个条件即可求出结论.
.所以对函数求导,根据斜率为1以及过点(1,0)两个条件即可求出结论.
(2)由函数 ,对函数
,对函数 求导,并令
求导,并令 可解得两个根,由于函数
可解得两个根,由于函数 在区间
在区间 内有且仅有一个极值点,
内有且仅有一个极值点, 的根在
的根在 内有且仅有一个根.所以通过分类讨论即可求
内有且仅有一个根.所以通过分类讨论即可求 的取值范围.
的取值范围.
(3)两曲线在交点 处的切线分别为
处的切线分别为 .若取
.若取 ,当直线
,当直线 与
与 轴围成等腰三角形时.通过求导求出两函数的切线的斜率,即可得到这两斜率不可能是相等,所以依题意可得到两切线倾斜角有两倍的关系,再通过解方程和函数的单调性的判断即可得到结论.
轴围成等腰三角形时.通过求导求出两函数的切线的斜率,即可得到这两斜率不可能是相等,所以依题意可得到两切线倾斜角有两倍的关系,再通过解方程和函数的单调性的判断即可得到结论.
(1) ,∴
,∴ ,又
,又 ,
,
∴ . 3分
. 3分
(2) ;
;
∴
由 得
得 ,
,
∴ 或
或 . 5分
. 5分
∵ ,当且仅当
,当且仅当 或
或 时,函数
时,函数 在区间
在区间 内有且仅有一个极值点. 6分
内有且仅有一个极值点. 6分
若 ,即
,即 ,当
,当 时
时 ;当
;当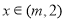 时
时 ,函数
,函数 有极大值点
有极大值点 ,
,
若 ,即
,即 时,当
时,当 时
时 ;当
;当 时
时 ,函数
,函数 有极大值点
有极大值点 ,
,
综上, 的取值范围是
的取值范围是 . 8分
. 8分
(3)当 时,设两切线
时,设两切线 的倾斜角分别为
的倾斜角分别为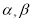 ,
,
则 ,
,
∵ , ∴
, ∴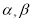 均为锐角, 9分
均为锐角, 9分
当 ,即
,即 时,若直线
时,若直线 能与
能与 轴围成等腰三角形,则
轴围成等腰三角形,则 ;当
;当 ,即
,即 时,若直线
时,若直线 能与
能与 轴围成等腰三角形,则
轴围成等腰三角形,则 .
.
由 得,
得, ,
,
得 ,即
,即 ,
,
此方程有唯一解 ,直线
,直线 能与
能与 轴围成一个等腰三角形. 11分
轴围成一个等腰三角形. 11分
由 得,
得,  ,
,
得 ,即
,即 ,
,
设 ,
, ,
,
当 时,
时, ,∴
,∴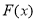 在
在 单调递增,则
单调递增,则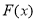 在
在 单调递
单调递
增,由于 ,且
,且 ,所以
,所以 ,则
,则 ,
,
即方程 在
在 有唯一解,直线
有唯一解,直线 能与
能与 轴围成一个等腰三角形.
轴围成一个等腰三角形.
因此,当 时,有两处符合题意,所以直线
时,有两处符合题意,所以直线 能与
能与 轴围成等腰三角形时,
轴围成等腰三角形时, 值的个数
值的个数
有2个. 14分
考点:1.导数的几何意义.2.函数的极值.3.函数导数的应用.4.分析问题解决问题的能力.5.等价变换的数学思想.


科目:高中数学 来源:2013-2014学年福建省厦门市高三5月适应性考试理科数学试卷(解析版) 题型:选择题
已知圆 和圆
和圆 ,动圆M与圆
,动圆M与圆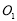 ,圆
,圆 都相切,动圆的圆心M的轨迹为两个椭圆,这两个椭圆的离心率分别为
都相切,动圆的圆心M的轨迹为两个椭圆,这两个椭圆的离心率分别为 ,
, (
(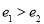 ),则
),则 的最小值是( )
的最小值是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省厦门市高三5月适应性考试文科数学试卷(解析版) 题型:选择题
设向量 与
与 满足
满足 ,
, 在
在 方向上的投影为
方向上的投影为 ,若存在实数
,若存在实数 ,使得
,使得 与
与 垂直,则
垂直,则 =( )
=( )
A. B.1 C. 2 D. 3
B.1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省厦门市高三5月适应性考试文科数学试卷(解析版) 题型:选择题
某市有大型超市200家、中型超市400家、小型超市1400家,为掌握各类超市的营业情况,现按分层抽样方法抽取一个容量为100的样本,应抽取中型超市( )
A. 70家 B.50家 C.20家 D.10家
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省三明市高三5月质量检查理科数学试卷(解析版) 题型:填空题
对于集合 ,如果定义了一种运算“
,如果定义了一种运算“ ”,使得集合
”,使得集合 中的元素间满足下列4个条件:
中的元素间满足下列4个条件:
(ⅰ) ,都有
,都有 ;
;
(ⅱ) ,使得对
,使得对 ,都有
,都有 ;
;
(ⅲ) ,
,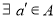 ,使得
,使得 ;
;
(ⅳ) ,都有
,都有 ,
,
则称集合 对于运算“
对于运算“ ”构成“对称集”.
”构成“对称集”.
下面给出三个集合及相应的运算“ ”:
”:
① ,运算“
,运算“ ”为普通加法;
”为普通加法;
② ,运算“
,运算“ ”为普通减法;
”为普通减法;
③ ,运算“
,运算“ ”为普通乘法.
”为普通乘法.
其中可以构成“对称集”的有 .(把所有正确的序号都填上)
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省三明市高三5月质量检查理科数学试卷(解析版) 题型:选择题
如图是某个四面体的三视图,若在该四面体的外接球内任取一点,则点落在四面体内的概率为( )
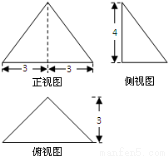
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年甘肃省武威市高三数学专题训练选择填空限时练六(解析版) 题型:选择题
采用系统抽样方法从480人中抽取16人做问卷调查,为此将他们随机编号为1,2,…,480,分组后在第一组采用简单随机抽样的方法抽到的号码为8.抽到的16人中,编号落入区间[1,160]的人做问卷A,编号落入区间[161,320]的人做问卷B,其余的人做问卷C,则被抽到的人中,做问卷B的人数为( )
A.4 B.5 C.6 D.7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com