
 (a>0,b>0)的离心率
(a>0,b>0)的离心率 ,过点A(0,-b)和B(a,0)的直线与原点的距离是
,过点A(0,-b)和B(a,0)的直线与原点的距离是 .
.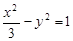 ,
,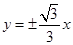 ;(Ⅱ)
;(Ⅱ) =
=
 ,∴
,∴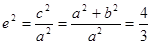 ,∴
,∴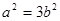 ①,直线
①,直线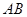 的方程为
的方程为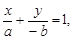 即
即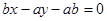 ,利用点到直线的距离公式得到:
,利用点到直线的距离公式得到: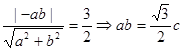 ②,两式联立,可求出
②,两式联立,可求出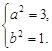 ,∴双曲线方程为
,∴双曲线方程为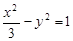 ,渐近线方程为:
,渐近线方程为: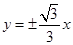 ;(Ⅱ)
;(Ⅱ)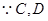 两点在以
两点在以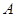 为圆心的同一个圆上,
为圆心的同一个圆上,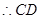 的中垂线过点
的中垂线过点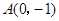 ,将直线
,将直线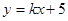 与双曲线
与双曲线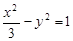 联立,消去
联立,消去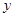 ,可得
,可得 ,设
,设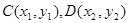 ,中点为
,中点为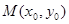 ,则
,则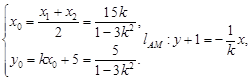 ∴
∴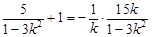 ,解得
,解得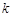 =
=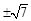 ,并检验是否满足(
,并检验是否满足(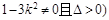 .
.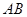 的方程为:
的方程为: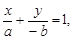 即
即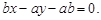
 到直线
到直线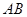 的距离
的距离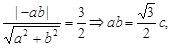
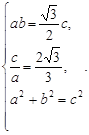 得
得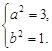 3分
3分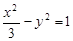 4分
4分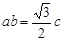 )
)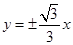 5分
5分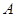 (0,-1),设
(0,-1),设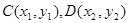 ,由
,由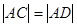
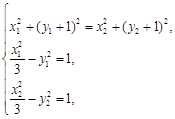 7分
7分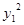 +
+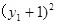 =3+3
=3+3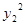 +
+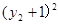 ,
,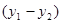
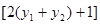 =0,
=0, 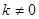 ,∴
,∴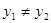 ,∴
,∴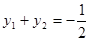 ,
, 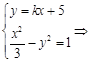
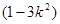
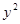 -10
-10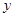 +25-3
+25-3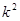 =0 (
=0 (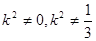 ),
),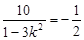 , 10分
, 10分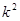 =7, 11分
=7, 11分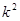 )(25-3
)(25-3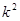 )>0
)>0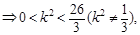
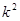 =7满足此条件,
=7满足此条件,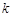 =
=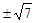 . 12分
. 12分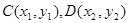 ,中点为
,中点为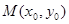 ,
,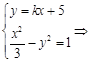
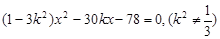 , 7分
, 7分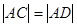 ,
,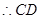 的中垂线过点
的中垂线过点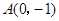 9分
9分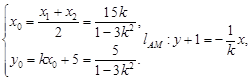 ∴
∴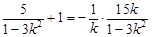 11分
11分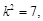 解得
解得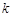 =
=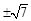 .(
.(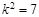 满足
满足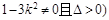 12分
12分

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案科目:高中数学 来源:不详 题型:单选题
| A.圆 | B.椭圆 | C.双曲线的一支 | D.抛物线 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com