
分析 (Ⅰ)利用导数的运算法则求出f′(x),求出切线斜率,即可求f(x)在点(0,f(0))处的切线方程;
(Ⅱ)当f(x1)=f(x2)(x1≠x2)时,不妨设x1<x2.由(I)可知:x1∈(-∞,0),x2∈(0,1).利用导数先证明:?x∈(0,1),f(x)<f(-x).而x2∈(0,1),可得f(x2)<f(-x2).即f(x1)<f(-x2).由于x1,-x2∈(-∞,0),f(x)在(-∞,0)上单调递增,因此得证.
解答 (Ⅰ)解:∵$f(x)=\frac{1-x}{1+{x}^{2}}{e}^{x}$,
∴f′(x)=$\frac{-x[(x-1)^{2}+2]}{(1+{x}^{2})^{2}}{e}^{x}$,
∴f′(0)=0,f(0)=1
∴f(x)在点(0,f(0))处的切线方程为y=1;
(Ⅱ)证明:当x<1时,由于$\frac{1-x}{1+{x}^{2}}$>0,ex>0,得到f(x)>0;
同理,当x>1时,f(x)<0.
当f(x1)=f(x2)(x1≠x2)时,不妨设x1<x2.
当x<0时,f′(x)>0;当x>0时,f′(x)<0.
∴函数f(x)的单调递增区间为(-∞,0),单调递减区间为(0,+∞).
可知:x1∈(-∞,0),x2∈(0,1).
下面证明:?x∈(0,1),f(x)<f(-x),即证$\frac{1-x}{1+{x}^{2}}$<$\frac{1+x}{1+{x}^{2}}{e}^{-x}$.
此不等式等价于(1-x)ex-$\frac{1+x}{{e}^{x}}$<0.
令g(x)=(1-x)ex-$\frac{1+x}{{e}^{x}}$,则g′(x)=-xe-x(e2x-1).
当x∈(0,1)时,g′(x)<0,g(x)单调递减,∴g(x)<g(0)=0.
即(1-x)ex-$\frac{1+x}{{e}^{x}}$<0.
∴?x∈(0,1),f(x)<f(-x).
而x2∈(0,1),∴f(x2)<f(-x2).
从而,f(x1)<f(-x2).
由于x1,-x2∈(-∞,0),f(x)在(-∞,0)上单调递增,
∴x1<-x2,即x1+x2<0.
点评 本题综合考查了利用导数研究切线方程、函数的单调性、等价转化问题等基础知识与基本技能,需要较强的推理能力和计算能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | lg(x2+$\frac{1}{4}$)>lgx(x>0) | B. | sin x+$\frac{1}{sinx}$≥2(x≠$\frac{kπ}{2}$,k∈Z) | ||
| C. | x2+1≥2|x|(x∈R) | D. | $\frac{1}{{x}^{2}+1}$>1(x∈R) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{2}({2}^{n}-1)$ | B. | $\frac{5}{18}({3}^{n}-1)$ | C. | $5•{2}^{n-1}-\frac{5}{4}$ | D. | $5•{2}^{n-2}-\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
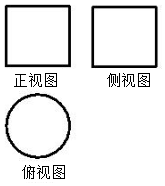
| A. | 6π | B. | $8\sqrt{2}$π | C. | $4+4\sqrt{2}$π | D. | $8+4\sqrt{2}$π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com