
(本题满分12分)
已知f (x)=sinx+ cosx (xÎR).
cosx (xÎR).
(Ⅰ)求函数f (x)的周期和最大值;
(Ⅱ)若f (A+ )=
)= ,求cos2A的值.
,求cos2A的值.
(Ⅰ) x=2kp+ (kÎZ),f (x)的最大值为2.(Ⅱ)-
(kÎZ),f (x)的最大值为2.(Ⅱ)-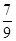 .
.
解析试题分析:(Ⅰ) f (x)=2sin(x+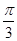 ),∴最小正周期T=2p.……3分
),∴最小正周期T=2p.……3分
当x+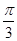 =2kp+
=2kp+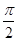 时,即x=2kp+
时,即x=2kp+ (kÎZ),f (x)的最大值为2.……6分
(kÎZ),f (x)的最大值为2.……6分
(Ⅱ)f (A+ )=2sin(A+
)=2sin(A+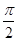 )=2cosA=
)=2cosA= ,∴cosA=
,∴cosA= .……9分
.……9分
cos2A=2cos2A-1=-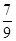 .……12分
.……12分
考点:本题主要考查三角函数诱导公式,三角函数和差倍半公式,三角函数的性质。
点评:典型题,在利用三角函数恒等变换解题过程中,“变角、变号、变名”是常用技巧,为研究三角函数的性质,往往要先将函数“化一”。(2)小题首先求得cosA,利用倍角公式求得cos2A。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知函数 的图像上两相邻最高点的坐标分别为
的图像上两相邻最高点的坐标分别为 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,且 求
求 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
如图,用半径为R的圆铁皮,剪一个圆心角为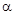 的扇形,制成一个圆锥形的漏斗,问圆心角
的扇形,制成一个圆锥形的漏斗,问圆心角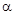 取什么值时,漏斗容积最大.(圆锥体积公式:
取什么值时,漏斗容积最大.(圆锥体积公式: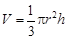 ,其中圆锥的底面半径为r,高为h)
,其中圆锥的底面半径为r,高为h)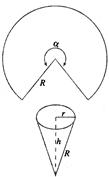
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)已知 ,函数
,函数 (其中
(其中 的图像在
的图像在 轴右侧的第一个最高点(即函数取得最大值的点)为
轴右侧的第一个最高点(即函数取得最大值的点)为
 ,在原点右侧与
,在原点右侧与 轴的第一个交点为
轴的第一个交点为
 .
.
(1)求函数 的表达式;
的表达式;
(2)判断函数 在区间
在区间 上是否存在对称轴,存在求出方程;否则说明理由;
上是否存在对称轴,存在求出方程;否则说明理由;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com