
°æƒø°ø¿¨ª¯∑÷¿ý «∂‘¿¨ª¯Ω¯––”––ߥ¶÷√µƒ“ª÷÷ø∆—ßπпÌ∑Ω∑®£¨Œ™¡À¡ÀΩ‚æ”√Ò∂‘¿¨ª¯∑÷¿ýµƒ÷™œ˛¬ ∫Õ≤Œ”ά £¨“˝µºæ”√Òª˝º´––∂Ø£¨ø∆—ßµÿΩ¯––¿¨ª¯∑÷¿ý£¨ƒ≥–°«¯Àʪ˙≥È»°ƒÍ¡‰‘⁄«¯º‰[25£¨85]…œµƒ50»ÀΩ¯––µ˜—–£¨Õ≥º∆≥ˆƒÍ¡‰∆µ ˝∑÷≤ºº∞¡ÀΩ‚¿¨ª¯∑÷¿ýµƒ»À ˝»Á±Ì£∫

£®1£©ÃÓ–¥œ¬√Ê2x2¡–¡™±Ì£¨≤¢≈–∂œƒÐ∑Ò‘⁄∑∏¥ÌŒÛµƒ∏≈¬ ≤ª≥¨π˝0.01µƒ«∞÷œ¬»œŒ™“‘65ÀÍŒ™∑÷ΩÁµ„æ”√Ò∂‘¡ÀΩ‚¿¨ª¯∑÷¿ýµƒ”–πÿ÷™ ∂”–≤Ó“Ï£ª
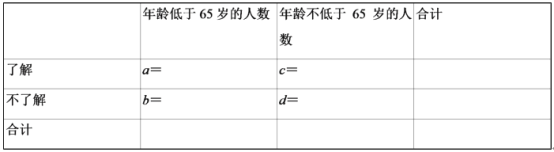
£®2£©»Ù∂‘ƒÍ¡‰‘⁄[45£¨55£©£¨[25£¨35£©µƒ±ªµ˜—–»À÷–∏˜Àʪ˙—°»°2»ÀΩ¯––…ӻε˜—–£¨º«—°÷–µƒ4»À÷–≤ª¡ÀΩ‚¿¨ª¯∑÷¿ýµƒ»À ˝Œ™X£¨«ÛÀʪ˙±‰¡øXµƒ∑÷≤º¡–∫Õ ˝—ß∆⁄Õ˚.
≤Œøºπ´ Ω∫Õ ˝æðK2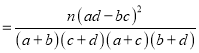 £¨∆‰÷–n£Ωa+b+c+d.
£¨∆‰÷–n£Ωa+b+c+d.

°æ¥∞∏°ø£®1£©Ãӱ̺˚Ω‚Œˆ£ª≤ªƒÐ£®2£©∑÷≤º¡–º˚Ω‚Œˆ£ª∆⁄Õ˚Œ™![]()
°æΩ‚Œˆ°ø
£®1£©∏˘æð“‚ÃÓ–¥¡–¡™±Ì£¨º∆À„π€≤‚÷µ£¨∂‘’’¡ŸΩÁ÷µµ√≥ˆΩ·¬€£ª
£®2£©”…“‚÷™Àʪ˙±‰¡øXµƒø…ƒÐ»°÷µ£¨º∆À„∂‘”¶µƒ∏≈¬ ÷µ£¨–¥≥ˆ∑÷≤º¡–£¨«Û≥ˆ ˝—ß∆⁄Õ˚÷µ.
Ω‚£∫£®1£©∏˘æð“‚ÃÓ–¥2x2¡–¡™±Ì£¨

º∆À„K2![]() 6.272£º6.635£¨
6.272£º6.635£¨
À˘“‘≤ªƒÐ‘⁄∑∏¥ÌŒÛµƒ∏≈¬ ≤ª≥¨π˝0.01µƒ«∞÷œ¬£¨»œŒ™“‘65ÀÍŒ™∑÷ΩÁµ„æ”√Ò∂‘¡ÀΩ‚¿¨ª¯∑÷¿ýµƒ”–πÿ÷™ ∂”–≤Ó“Ï£ª
£®2£©”…“‚÷™£¨Àʪ˙±‰¡øXµƒø…ƒÐ»°÷µŒ™0£¨1£¨2£¨3£ª
º∆À„P£®X£Ω0£©![]() £¨
£¨
P£®X£Ω1£©![]() £¨
£¨
P£®X£Ω2£©![]() £¨
£¨
P£®X£Ω3£©![]() £ª
£ª
À˘“‘Àʪ˙±‰¡øXµƒ∑÷≤º¡–Œ™£∫
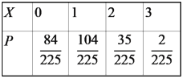
À˘“‘Xµƒ ˝—ß∆⁄Õ˚Œ™E£®X£©£Ω0![]() 1
1![]() 2
2![]() 3
3![]() .
.



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥∏þ÷–…ÁÕ≈Ω¯––…Áª· µº˘£¨∂‘[25£¨55]À͵ƒ»À»∫Àʪ˙≥È»°n»ÀΩ¯––¡À“ª¥Œ «∑Òø™Õ®°∞Œ¢≤©°±µƒµ˜≤È£¨»Ùø™Õ®°∞Œ¢≤©°±µƒ≥∆Œ™°∞ ±…–◊°±£¨∑Ò‘Ú≥∆Œ™°∞∑« ±…–◊°±£¨Õ®π˝µ˜≤È∑÷±µ√µΩ»ÁÕºÀ˘ æÕ≥º∆±Ì∫Õ∏˜ƒÍ¡‰∂Œ»À ˝∆µ¬ ∑÷≤º÷±∑ΩÕº£∫ 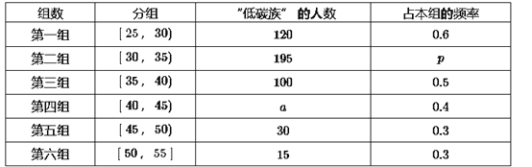
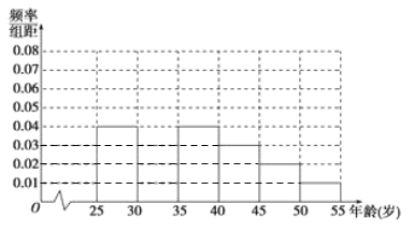
ÕÍ≥…“‘œ¬Œ £∫
£®¢Ò£©≤π»´∆µ¬ ∑÷≤º÷±∑ΩÕº≤¢«Ûn£¨a£¨pµƒ÷µ£ª
£®¢Ú£©¥”[40£¨50£©À̓͡‰∂Œµƒ°∞ ±…–◊°±÷–≤…”√∑÷≤„≥È—˘∑®≥È»°18»À≤Œº”Õ¯¬Á ±…–¥Ô»À¥Û»¸£¨∆‰÷–—°»°3»À◊˜Œ™¡Ï∂”£¨º«—°»°µƒ3√˚¡Ï∂”÷–ƒÍ¡‰‘⁄[40£¨45£©À͵ƒ»À ˝Œ™X£¨«ÛXµƒ∑÷≤º¡–∫Õ∆⁄Õ˚E£®X£©..
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝![]() .
.
£®1£©Ã÷¬€![]() µƒµ•µ˜–‘.
µƒµ•µ˜–‘.
£®2£© ‘Œ «∑ҥʑ⁄![]() £¨ πµ√
£¨ πµ√![]() ∂‘
∂‘![]() ∫„≥…¡¢£ø»Ù¥Ê‘⁄£¨«Û
∫„≥…¡¢£ø»Ù¥Ê‘⁄£¨«Û![]() µƒ»°÷µ∑∂Œß£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”….
µƒ»°÷µ∑∂Œß£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”….
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄Àƒ¿‚◊∂![]() ÷–£¨
÷–£¨![]() ∆Ω√Ê
∆Ω√Ê![]() ∆Ω√Ê
∆Ω√Ê![]() £¨
£¨![]() «
«![]() µƒ÷–µ„£¨
µƒ÷–µ„£¨![]() «
«![]() …œ“ªµ„£¨«“
…œ“ªµ„£¨«“![]()
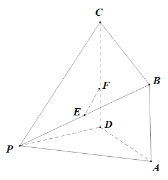
£®1£©«Û÷§:![]() ∆Ω√Ê
∆Ω√Ê![]() £ª
£ª
£®2£©»Ù![]() «Û÷±œþ
«Û÷±œþ![]() ”Î∆Ω√Ê
”Î∆Ω√Ê![]() À˘≥…Ω«µƒ’˝œ“÷µ.
À˘≥…Ω«µƒ’˝œ“÷µ.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄»´√Êøπª˜–¬π⁄∑Œ—◊“þ«È’‚“ªÃÿ ‚ ±∆⁄£¨Œ“ –ΩÔ˝æ÷÷≥ˆ°∞Õ£øŒ≤ªÕ£—ß°±µƒø⁄∫≈£¨πƒ¿¯—ß…˙œþ…œ—ßœ∞.ƒ≥–£ ˝—ßΩà ¶Œ™¡Àµ˜≤È∏þ»˝—ß…˙ ˝—ß≥…º®”Îœþ…œ—ßœ∞ ±º‰÷ƺ‰µƒœýπÿπÿœµ£¨∂‘∏þ»˝ƒÍº∂Àʪ˙—°»°45√˚—ß…˙Ω¯––∏˙◊ŸŒ æÌ£¨∆‰÷–√ø÷Ðœþ…œ—ßœ∞ ˝—ß ±º‰≤ª…Ÿ”⁄5–° ±µƒ”–19»À£¨”ýœ¬µƒ»À÷–£¨‘⁄ºÏ≤‚øº ‘÷– ˝—ß∆Ωæ˘≥…º®≤ª◊„120∑÷µƒ’º![]() £¨Õ≥º∆≥…º®∫Ûµ√µΩ»Áœ¬
£¨Õ≥º∆≥…º®∫Ûµ√µΩ»Áœ¬![]() ¡–¡™±Ì£∫
¡–¡™±Ì£∫
∑÷ ˝≤ª…Ÿ”⁄120∑÷ | ∑÷ ˝≤ª◊„120∑÷ | ∫œº∆ | |
œþ…œ—ßœ∞ ±º‰≤ª…Ÿ”⁄5–° ± | 4 | 19 | |
œþ…œ—ßœ∞ ±º‰≤ª◊„5–° ± | |||
∫œº∆ | 45 |
£®1£©«ÎÕÍ≥……œ√Ê![]() ¡–¡™±Ì£ª≤¢≈–∂œ «∑Ò”–99%µƒ∞—Œ’»œŒ™°∞∏þ»˝—ß…˙µƒ ˝—ß≥…º®”Η߅˙œþ…œ—ßœ∞ ±º‰”–πÿ°±£ª
¡–¡™±Ì£ª≤¢≈–∂œ «∑Ò”–99%µƒ∞—Œ’»œŒ™°∞∏þ»˝—ß…˙µƒ ˝—ß≥…º®”Η߅˙œþ…œ—ßœ∞ ±º‰”–πÿ°±£ª
£®2£©‘⁄…œ ˆ—˘±æ÷–¥”∑÷ ˝≤ª…Ÿ”⁄120∑÷µƒ—ß…˙÷–£¨∞¥’’∑÷≤„≥È—˘µƒ∑Ω∑®£¨≥ÈµΩœþ…œ—ßœ∞ ±º‰≤ª…Ÿ”⁄5–° ±∫Õœþ…œ—ßœ∞ ±º‰≤ª◊„5–° ±µƒ—ß…˙π≤5√˚£¨»Ù‘⁄’‚5√˚—ß…˙÷–Àʪ˙≥È»°2»À£¨«Û÷¡…Ÿ1»À√ø÷Ðœþ…œ—ßœ∞ ±º‰≤ª◊„5–° ±µƒ∏≈¬ .
£®œ¬√ʵƒ¡ŸΩÁ÷µ±Ìπ©≤Œøº£©
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
£®≤Œøºπ´ Ω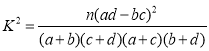 ∆‰÷–
∆‰÷–![]() £©
£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
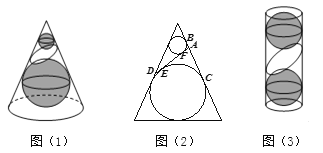
°æƒø°ø»ÁÕº£®1£©£¨‘⁄‘≤◊∂ƒ⁄∑≈¡Ω∏ˆ¥Û–°≤ªÕ¨«“≤ªœý«–µƒ«Ú, πµ√À¸√«∑÷±”Α≤◊∂µƒ≤ý√Ê°¢µ◊√Êœý«–£¨”√”Î¡Ω«Ú∂ºœý«–µƒ∆Ω√ÊΩÿ‘≤◊∂µƒ≤ý√ʵ√µΩΩÿø⁄«˙œþ «Õ÷‘≤.¿Ì”…»Áœ¬£∫»ÁÕº£®2£©£¨»Ù¡Ω∏ˆ«Ú∑÷±”ÎΩÿ√Êœý«–”⁄µ„![]() £¨‘⁄µ√µΩµƒΩÿø⁄«˙œþ…œ»Œ»°“ªµ„
£¨‘⁄µ√µΩµƒΩÿø⁄«˙œþ…œ»Œ»°“ªµ„![]() £¨π˝µ„
£¨π˝µ„![]() ◊˜‘≤◊∂ƒ∏œþ£¨∑÷±”Î¡Ω«Úœý«–”⁄µ„
◊˜‘≤◊∂ƒ∏œþ£¨∑÷±”Î¡Ω«Úœý«–”⁄µ„![]() £¨”…«Ú”Α≤µƒº∏∫Œ–‘÷ £¨µ√
£¨”…«Ú”Α≤µƒº∏∫Œ–‘÷ £¨µ√![]() £¨
£¨![]() £¨À˘“‘
£¨À˘“‘![]() £¨«“
£¨«“![]() £¨”…Õ÷‘≤∂®“Â÷™Ωÿø⁄«˙œþ «Õ÷‘≤£¨«–µ„
£¨”…Õ÷‘≤∂®“Â÷™Ωÿø⁄«˙œþ «Õ÷‘≤£¨«–µ„![]() Œ™Ωπµ„.’‚∏ˆΩ·¬€‘⁄‘≤÷˘÷–“≤ ”√£¨»ÁÕº£®3£©£¨‘⁄“ª∏ˆ∏þŒ™
Œ™Ωπµ„.’‚∏ˆΩ·¬€‘⁄‘≤÷˘÷–“≤ ”√£¨»ÁÕº£®3£©£¨‘⁄“ª∏ˆ∏þŒ™![]() £¨µ◊√Ê∞Îæ∂Œ™
£¨µ◊√Ê∞Îæ∂Œ™![]() µƒ‘≤÷˘Ãƒ⁄∑≈«Ú£¨«Ú”Α≤÷˘µ◊√ʺ∞≤ý√Êæ˘œý«–.»Ù“ª∏ˆ∆Ω√ʔΡΩ∏ˆ«Úæ˘œý«–£¨‘Ú¥À∆Ω√ÊΩÿ‘≤÷˘À˘µ√µƒΩÿø⁄«˙œþ“≤Œ™“ª∏ˆÕ÷‘≤£¨‘Ú∏√Õ÷‘≤µƒ¿Î–ƒ¬ Œ™______.
µƒ‘≤÷˘Ãƒ⁄∑≈«Ú£¨«Ú”Α≤÷˘µ◊√ʺ∞≤ý√Êæ˘œý«–.»Ù“ª∏ˆ∆Ω√ʔΡΩ∏ˆ«Úæ˘œý«–£¨‘Ú¥À∆Ω√ÊΩÿ‘≤÷˘À˘µ√µƒΩÿø⁄«˙œþ“≤Œ™“ª∏ˆÕ÷‘≤£¨‘Ú∏√Õ÷‘≤µƒ¿Î–ƒ¬ Œ™______.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº¢Ÿ£¨Àƒ±þ–Œ![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() Œ™
Œ™![]() µƒ÷–µ„.Ω´
µƒ÷–µ„.Ω´![]() —ÿ
—ÿ![]() ’€∆µΩ
’€∆µΩ![]() µƒŒª÷√£¨»ÁÕº¢⁄.
µƒŒª÷√£¨»ÁÕº¢⁄.
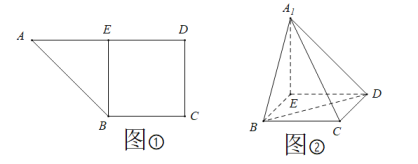
£®¢Ò£©«Û÷§£∫∆Ω√Ê![]() ∆Ω√Ê
∆Ω√Ê![]() £ª
£ª
£®¢Ú£©»Ù![]() £¨«Û
£¨«Û![]() ”Î∆Ω√Ê
”Î∆Ω√Ê![]() À˘≥…Ω«µƒ’˝œ“÷µ.
À˘≥…Ω«µƒ’˝œ“÷µ.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝f£®x£©£Ω|x+1|©Å|2x©Å2|µƒ◊Ó¥Û÷µŒ™M£¨’˝ µ ˝a£¨b¬˙◊„a+b£ΩM£Æ
£®1£©«Û2a2+b2µƒ◊Ó–°÷µ£ª
£®2£©«Û÷§£∫aabb°ðab£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∆Ω√ʜڡø![]() £¨
£¨![]() π≤œþµƒ≥‰“™Ãıº˛ «£® £©
π≤œþµƒ≥‰“™Ãıº˛ «£® £©
A.![]()
B.![]() £¨
£¨![]() ¡ΩœÚ¡ø÷–÷¡…Ÿ”–“ª∏ˆŒ™¡„œÚ¡ø
¡ΩœÚ¡ø÷–÷¡…Ÿ”–“ª∏ˆŒ™¡„œÚ¡ø
C.¶À° R£¨![]()
D.¥Ê‘⁄≤ª»´Œ™¡„µƒ µ ˝¶À1£¨¶À2£¨![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com