
【题目】某高中社团进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次是否开通“微博”的调查,若开通“微博”的称为“时尚族”,否则称为“非时尚族”,通过调查分别得到如图所示统计表和各年龄段人数频率分布直方图: 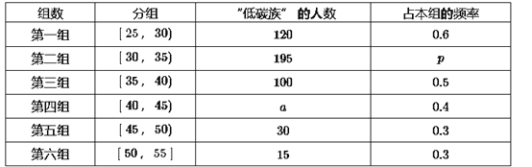
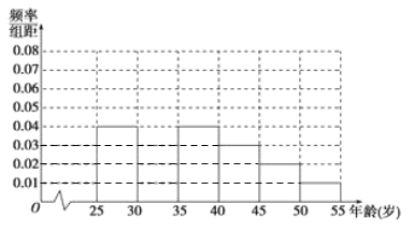
完成以下问题:
(Ⅰ)补全频率分布直方图并求n,a,p的值;
(Ⅱ)从[40,50)岁年龄段的“时尚族”中采用分层抽样法抽取18人参加网络时尚达人大赛,其中选取3人作为领队,记选取的3名领队中年龄在[40,45)岁的人数为X,求X的分布列和期望E(X)..
【答案】(1)直方图见解析,![]() (2)分布列见解析,
(2)分布列见解析,![]()
【解析】
试题(Ⅰ)根据所求矩形的面积和为1求出第二组的频率,然后求出高,画出频率直方图,求出第一组的人数和频率从而求出n,由题可知,第二组的频率以及人数,从而求出p的值,然后求出第四组的频率和人数从而求出a的值;
(Ⅱ)因为[40,45)岁年龄段的“时尚族”与[45,50)岁年龄段的“时尚族”的比值为2:1,所以采用分层抽样法抽取18人,[40,45)岁中有12人,[45,50)岁中有6人,机变量X服从超几何分布,X的取值可能为0,1,2,3,分别求出相应的概率,列出分布列,根据数学期望公式求出期望即可.
试题解析:解:(Ⅰ)第二组的频率为1-(0.04+0.04+0.03+0.02+0.01)×5=0.3,
所以高为![]() . 频率直方图如下:
. 频率直方图如下:
第一组的人数为![]() ,频率为0.04×5=0.2,所以
,频率为0.04×5=0.2,所以![]() .
.
由题可知,第二组的频率为0.3,所以第二组的人数为1000×0.3=300, 所以![]() .
.
第四组的频率为0.03×5=0.15,所以第四组的人数为1000×0.15=150, 所以a=150×0.4=60.
(Ⅱ)因为[40,45)岁年龄段的“时尚族”与[45,50)岁年龄段的“时尚族”的比值
为60:30=2:1,所以采用分层抽样法抽取18人,[40,45)岁中有12人,[45,50)岁中有6人.
随机变量X服从超几何分布.![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以随机变量X的分布列为
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
∴数学期望![]() (或者
(或者 ![]() ).
).


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() ,
,![]() ,给出以下四个命题:①
,给出以下四个命题:①![]() 为偶函数;②
为偶函数;②![]() 为偶函数;③
为偶函数;③![]() 的最小值为0;④
的最小值为0;④![]() 有两个零点.其中真命题的是( ).
有两个零点.其中真命题的是( ).
A.②④B.①③C.①③④D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() .其中
.其中![]() ,
,![]() 表示直线,
表示直线,![]() 、β表示平面,给出如下5个命题:
、β表示平面,给出如下5个命题:
①若![]() //
//![]() ,则
,则![]() //
//![]() ;
;
②若![]() ⊥
⊥![]() ,则
,则![]() ⊥
⊥![]() ;
;
③![]() 与
与![]() 不垂直,则
不垂直,则![]() 不可能成立;
不可能成立;
④若![]() ,则
,则![]() ;
;
⑤![]() ,则
,则![]() ;
;
其中真命题的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为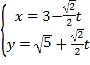 (
(![]() 为参数),在以坐标原点
为参数),在以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴的极坐标中,圆
轴正半轴为极轴的极坐标中,圆![]() 的方程为
的方程为![]() .
.
(1)写出直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 的坐标为
的坐标为![]() ,圆
,圆![]() 与直线
与直线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年,某省将实施新高考,
年,某省将实施新高考,![]() 年秋季入学的高一学生是新高考首批考生,新高考不再分文理科,采用
年秋季入学的高一学生是新高考首批考生,新高考不再分文理科,采用![]() 模式,其中语文、数学、外语三科为必考科目,满分各
模式,其中语文、数学、外语三科为必考科目,满分各![]() 分,另外,考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物
分,另外,考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物![]() 门科目中自选
门科目中自选![]() 门参加考试(
门参加考试(![]() 选
选![]() ),每科目满分
),每科目满分![]() 分.为了应对新高考,某高中从高一年级
分.为了应对新高考,某高中从高一年级![]() 名学生(其中男生
名学生(其中男生![]() 人,女生
人,女生![]() 人)中,采用分层抽样的方法从中抽取n名学生进行调查.
人)中,采用分层抽样的方法从中抽取n名学生进行调查.
(1)已知抽取的n名学生中含女生![]() 人,求n的值及抽取到的男生人数;
人,求n的值及抽取到的男生人数;
(2)学校计划在高一上学期开设选修中的“物理”和“历史”两个科目,为了了解学生对这两个科目的选课情况,对在(1)的条件下抽取到的![]() 名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目),下面表格是根据调查结果得到的
名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目),下面表格是根据调查结果得到的![]() 列联表,请将下面的列联表补充完整,并判断是否有
列联表,请将下面的列联表补充完整,并判断是否有![]() 的把握认为选择科目与性别有关?说明你的理由;
的把握认为选择科目与性别有关?说明你的理由;
选择“物理” | 选择“历史” | 总计 | |
男生 | 10 | ||
女生 | 30 | ||
总计 |
(3)在抽取到的![]() 名女生中,在(2)的条件下,按选择的科目进行分层抽样,抽出
名女生中,在(2)的条件下,按选择的科目进行分层抽样,抽出![]() 名女生,了解女生对“历史”的选课意向情况,在这
名女生,了解女生对“历史”的选课意向情况,在这![]() 名女生中再抽取
名女生中再抽取![]() 人,求这
人,求这![]() 人中选择“历史”的人数为
人中选择“历史”的人数为![]() 人的概率.
人的概率.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() 的离心率为
的离心率为![]() ,双曲线
,双曲线![]() 的渐近线与椭圆
的渐近线与椭圆![]() 的交点到原点的距离均为
的交点到原点的距离均为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若点![]() 为椭圆
为椭圆![]() 上的动点,
上的动点,![]() 三点共线,直线
三点共线,直线![]() 的斜率分别为
的斜率分别为![]() .
.
(i)证明:![]() ;
;
(ii)若![]() ,设直线
,设直线![]() 过点
过点![]() ,直线
,直线![]() 过点
过点![]() ,证明:
,证明:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点![]() 是以
是以![]() 为直径的圆上的动点(异于
为直径的圆上的动点(异于![]() ,
,![]() ),已知
),已知![]() ,
,![]() ,
,![]() 平面
平面![]() ,四边形
,四边形![]() 为平行四边形.
为平行四边形.
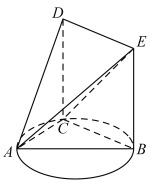
(1)求证:![]() 平面
平面![]() ;
;
(2)当三棱锥![]() 的体积最大时,求平面
的体积最大时,求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】垃圾分类是对垃圾进行有效处置的一种科学管理方法,为了了解居民对垃圾分类的知晓率和参与率,引导居民积极行动,科学地进行垃圾分类,某小区随机抽取年龄在区间[25,85]上的50人进行调研,统计出年龄频数分布及了解垃圾分类的人数如表:

(1)填写下面2x2列联表,并判断能否在犯错误的概率不超过0.01的前提下认为以65岁为分界点居民对了解垃圾分类的有关知识有差异;
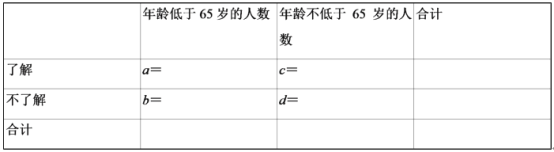
(2)若对年龄在[45,55),[25,35)的被调研人中各随机选取2人进行深入调研,记选中的4人中不了解垃圾分类的人数为X,求随机变量X的分布列和数学期望.
参考公式和数据K2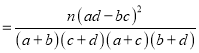 ,其中n=a+b+c+d.
,其中n=a+b+c+d.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com