
【题目】已知![]() .其中
.其中![]() ,
,![]() 表示直线,
表示直线,![]() 、β表示平面,给出如下5个命题:
、β表示平面,给出如下5个命题:
①若![]() //
//![]() ,则
,则![]() //
//![]() ;
;
②若![]() ⊥
⊥![]() ,则
,则![]() ⊥
⊥![]() ;
;
③![]() 与
与![]() 不垂直,则
不垂直,则![]() 不可能成立;
不可能成立;
④若![]() ,则
,则![]() ;
;
⑤![]() ,则
,则![]() ;
;
其中真命题的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
根据线面位置关系,逐项判断,即可求得答案.
对①,根据两个平面相互平行,一个平面内的直线平行于另一平面,由![]() ,
,![]() //
//![]() ,则
,则![]() //
//![]() ,故①是真命题;
,故①是真命题;
对②,根据一个平面内的一条直线垂直另一个平面内的两条相交线,则这两个平面垂直,所以由![]() ⊥
⊥![]() ,不能推出
,不能推出![]() ⊥
⊥![]() ,故②假命题;
,故②假命题;
对③,画出正方体图象:
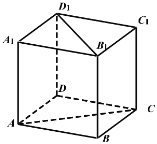
面![]() 面
面![]() ,
,
根据正方体特征可得:![]() ,
,
故:![]() 与
与![]() 不垂直,则
不垂直,则![]() 可能成立,故③假命题;
可能成立,故③假命题;
对④,根据一个平面内的一条直线垂直另一个平面的两条相交线,则这两个平面垂直,所以由![]() ,不能推出
,不能推出![]() ,故④假命题;
,故④假命题;
对⑤,根据两个平面垂直,一个平面内的直线垂直于交线,这条直线也垂直于另一个平面,由![]() ,则
,则![]() ,故⑤是真命题.
,故⑤是真命题.
综上所述,①⑤是真命题
故选:C.


科目:高中数学 来源: 题型:
【题目】抛物线![]() ,
,![]() 为直线
为直线![]() 上的动点,过点
上的动点,过点![]() 作抛物线
作抛物线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,
,![]() .
.
(1)证明:直线![]() 过定点;
过定点;
(2)若以![]() 为圆心的圆与直线
为圆心的圆与直线![]() 相切,且切点为线段
相切,且切点为线段![]() 的中点,求该圆的面积.
的中点,求该圆的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的右顶点为
)的右顶点为![]() .左、右焦点分别为
.左、右焦点分别为![]() ,
,![]() ,过点
,过点![]() 且垂直于
且垂直于![]() 轴的直线交椭圆于点
轴的直线交椭圆于点![]() (
(![]() 在第象限),直线
在第象限),直线![]() 的斜率为
的斜率为![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 的直线与椭圆交于
的直线与椭圆交于![]() 、
、![]() 两点(
两点(![]() 、
、![]() 不与
不与![]() 、
、![]() 重合),若
重合),若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】赵爽是我国古代数学家、天文学家,大约公元222年,赵爽为《周髀算经》一书作序时,介绍了“勾股圆方图”,又称“赵爽弦图”(以弦为边长得到的正方形是由![]() 个全等的直角三角形再加上中间的一个小正方形组成的,如图(1)),类比“赵爽弦图”,可类似地构造如图(2)所示的图形,它是由
个全等的直角三角形再加上中间的一个小正方形组成的,如图(1)),类比“赵爽弦图”,可类似地构造如图(2)所示的图形,它是由![]() 个全等的三角形与中间的一个小正六边形组成的一个大正六边形,设
个全等的三角形与中间的一个小正六边形组成的一个大正六边形,设![]() ,若在大正六边形中随机取一点,则此点取自小正六边形的概率为( )
,若在大正六边形中随机取一点,则此点取自小正六边形的概率为( )
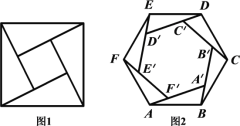
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂商调查甲、乙两种不同型号电视机在10个卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图.
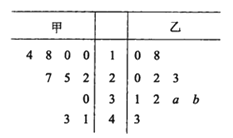
为了鼓励卖场,在同型号电视机的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”.
(1)当![]() 时,记甲型号电视机的“星级卖场”数量为
时,记甲型号电视机的“星级卖场”数量为![]() ,乙型号电视机的“星级卖场”数量为
,乙型号电视机的“星级卖场”数量为![]() ,比较
,比较![]() 的大小关系;
的大小关系;
(2)在这10个卖场中,随机选取2个卖场,记![]() 为其中甲型号电视机的“星级卖场”的个数,求
为其中甲型号电视机的“星级卖场”的个数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)若![]() ,记乙型号电视机销售量的方差为
,记乙型号电视机销售量的方差为![]() ,根据茎叶图推断
,根据茎叶图推断![]() 为何值时,
为何值时,![]() 达到最小值.(只需写出结论)
达到最小值.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中社团进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次是否开通“微博”的调查,若开通“微博”的称为“时尚族”,否则称为“非时尚族”,通过调查分别得到如图所示统计表和各年龄段人数频率分布直方图: 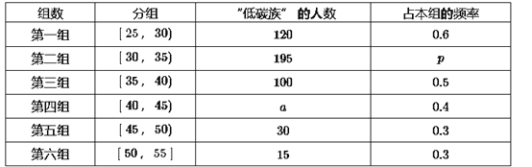
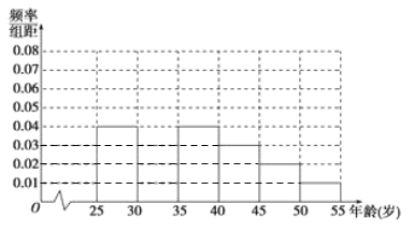
完成以下问题:
(Ⅰ)补全频率分布直方图并求n,a,p的值;
(Ⅱ)从[40,50)岁年龄段的“时尚族”中采用分层抽样法抽取18人参加网络时尚达人大赛,其中选取3人作为领队,记选取的3名领队中年龄在[40,45)岁的人数为X,求X的分布列和期望E(X)..
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com