
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
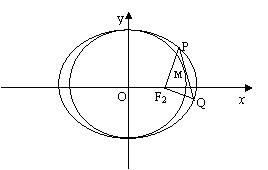
已知椭圆 的右焦点为F2(1,0),点
的右焦点为F2(1,0),点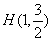 在椭圆上。
在椭圆上。
(1)求椭圆方程;
(2)点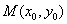 在圆
在圆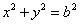 上,M在第一象限,过M作圆
上,M在第一象限,过M作圆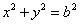 的切线交椭圆于P、Q两点,问|F2P|+|F2Q|+|PQ|是否为定值?如果是,求出定值,如不是,说明理由。
的切线交椭圆于P、Q两点,问|F2P|+|F2Q|+|PQ|是否为定值?如果是,求出定值,如不是,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
对直线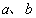 和平面
和平面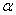 ,在
,在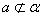 的前提下,给出关系:①
的前提下,给出关系:①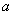 ∥
∥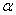 ,②
,②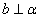 ,③
,③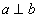 .以其中的两个关系作为条件,另一个关系作为结论可构造三个不同的命题,分别记为命题1、命题2、命题3.
.以其中的两个关系作为条件,另一个关系作为结论可构造三个不同的命题,分别记为命题1、命题2、命题3.
(Ⅰ)写出上述三个命题,并判断它们的真假;
(Ⅱ)选择(Ⅰ)中的一个真命题,根据题意画出图形,加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
在平面中,△ABC的角C的内角平分线CE分△ABC面积所成的比 =
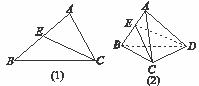
=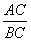 .将这个结论类比到空间:在三棱锥A-BCD中,平面DEC平分二面角A-CD-B且与AB交于E,则类比的结论为
.将这个结论类比到空间:在三棱锥A-BCD中,平面DEC平分二面角A-CD-B且与AB交于E,则类比的结论为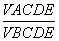 =________.
=________.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,半径为2的半圆有一内接梯形ABCD,它的下底AB是⊙O的直径,上底CD的端点在圆周上.若双曲线以A,B为焦点,且过C,D两点,则当梯形ABCD的周长最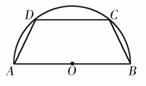 大时,双曲线的实轴长为
大时,双曲线的实轴长为
A.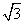 +1
+1
B.2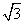 +2
+2
C.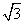 -1
-1
D.2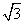 -2
-2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com