
如图,半径为2的半圆有一内接梯形ABCD,它的下底AB是⊙O的直径,上底CD的端点在圆周上.若双曲线以A,B为焦点,且过C,D两点,则当梯形ABCD的周长最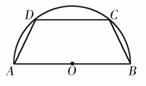 大时,双曲线的实轴长为
大时,双曲线的实轴长为
A.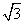 +1
+1
B.2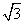 +2
+2
C.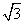 -1
-1
D.2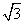 -2
-2
科目:高中数学 来源: 题型:
在正项等比数列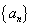 中,公比
中,公比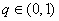 ,
,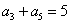 且
且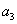 和
和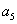 的等比中项是2.
的等比中项是2.
(1) 求数列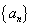 的通项公式;
的通项公式;
(2) 若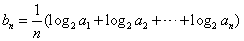 ,判断数列
,判断数列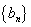 的前
的前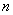 项和
项和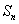 是否存在最大值,若存在,求出使
是否存在最大值,若存在,求出使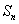 最大时
最大时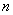 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
(Ⅰ)已知函数f(x)=ex-1-tx,∃x0∈R,使f(x0)≤0,求实数t的取值范围;
(Ⅱ)证明: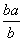 <ln
<ln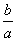 <
<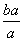 ,其中0<a<b;
,其中0<a<b;
(Ⅲ)设[x]表示不超过x的最大整数,证明:[ln(1+n)]≤[1+ +…+
+…+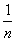 ]≤1+[lnn](n∈N*).
]≤1+[lnn](n∈N*).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com