
分析 (1)求出函数y的导数,可得切线的斜率,由切线方程可得a的方程,解得a即可;
(2)由题意可得即为$\frac{h({x}_{1})-2{x}_{1}-(h({x}_{2})-2{x}_{2})}{{x}_{1}-{x}_{2}}$>0,令m(x)=h(x)-2x,可得m(x)在(0,+∞)递增,求出导数,令导数大于等于0,分离参数a,由二次函数的最值,即可得到a的范围;
(3)原不等式等价于x0+$\frac{1}{{x}_{0}}$<alnx0-$\frac{a}{{x}_{0}}$,整理得x0-alnx0+$\frac{1+a}{{x}_{0}}$<0,设m(x)=x-alnx+$\frac{1+a}{x}$,求得它的导数m'(x),然后分a≤0、0<a≤e-1和a>e-1三种情况加以讨论,分别解关于a的不等式得到a的取值,最后综上所述可得实数a的取值范围是(-∞,-2)∪($\frac{{e}^{2}+1}{e-1}$,+∞).
解答 解:(1)y=f(x)-g(x)=$\frac{1}{2}$x2-alnx的导数为x-$\frac{a}{x}$,
曲线y=f(x)-g(x)在x=1处的切线斜率为k=1-a,
由切线的方程为6x-2y-5=0,可得1-a=3,
解得a=-2;
(2)h(x)=f(x)+g(x)=$\frac{1}{2}$x2+alnx,
对任意两个不等的正数x1,x2,都有$\frac{{h({x_1})-h({x_2})}}{{{x_1}-{x_2}}}$>2恒成立,即为
$\frac{h({x}_{1})-2{x}_{1}-(h({x}_{2})-2{x}_{2})}{{x}_{1}-{x}_{2}}$>0,
令m(x)=h(x)-2x,可得m(x)在(0,+∞)递增,
由m′(x)=h′(x)-2=x+$\frac{a}{x}$-2≥0恒成立,
可得a≥x(2-x)的最大值,由x(2-x)=-(x-1)2+1可得最大值1,
则a≥1,即a的取值范围是[1,+∞);
(3)不等式f′(x0)+$\frac{1}{{f'({x_0})}}$<g(x0)-g′(x0)等价于x0+$\frac{1}{{x}_{0}}$<alnx0-$\frac{a}{{x}_{0}}$,
整理得x0-alnx0+$\frac{1+a}{{x}_{0}}$<0,设m(x)=x-alnx+$\frac{1+a}{x}$,
则由题意可知只需在[1,e]上存在一点x0,使得m(x0)<0.
对m(x)求导数,得m′(x)=1-$\frac{a}{x}$-$\frac{1+a}{{x}^{2}}$=$\frac{{x}^{2}-ax-(1+a)}{{x}^{2}}$=$\frac{(x-a-1)(x+1)}{{x}^{2}}$,
因为x>0,所以x+1>0,令x-1-a=0,得x=1+a.
①若1+a≤1,即a≤0时,令m(1)=2+a<0,解得a<-2.
②若1<1+a≤e,即0<a≤e-1时,m(x)在1+a处取得最小值,
令m(1+a)=1+a-aln(1+a)+1<0,即1+a+1<aln(1+a),
可得$\frac{a+1+1}{a}$<ln(a+1)
考察式子$\frac{t+1}{t-1}$<lnt,因为1<t≤e,可得左端大于1,而右端小于1,所以不等式不能成立
③当1+a>e,即a>e-1时,m(x)在[1,e]上单调递减,只需m(e)<0,得a>$\frac{{e}^{2}+1}{e-1}$,
又因为e-1-$\frac{{e}^{2}+1}{e-1}$=$\frac{-2e}{e-1}$<0,则a>$\frac{{e}^{2}+1}{e-1}$.
综上所述,实数a的取值范围是(-∞,-2)∪($\frac{{e}^{2}+1}{e-1}$,+∞).
点评 本题给出二次函数和对数函数,求切线的方程和函数的单调性的运用,着重考查了导数的公式和运算法则、利用导数研究函数的单调性和导数在最大最小值问题中的应用等知识,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 7 | C. | 8 | D. | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
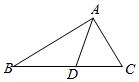 如图,在三角形ABC中,AB=2,AC=1,cos∠BAC=$\frac{1}{3}$,∠BAC的平分线交BC于点D.
如图,在三角形ABC中,AB=2,AC=1,cos∠BAC=$\frac{1}{3}$,∠BAC的平分线交BC于点D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1丈3尺 | B. | 5丈4尺 | C. | 9丈2尺 | D. | 48丈6尺 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com