Question

14．在△ABC中，D为AC的中点，$\overrightarrow{BC}$=3$\overrightarrow{BE}$，BD与 AE交于点F，若$\overrightarrow{AF}$=λ$\overrightarrow{AE}$，则实数λ的值为$\frac{3}{4}$．

Answer 1

分析 作EG∥AC交BD于G，根据平行线分线段成比例定理得到$\frac{EF}{FA}$=$\frac{1}{3}$，问题得以解决．

解答 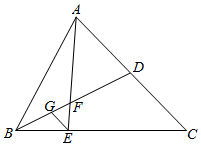解：作EG∥AC交BD于G，
∵$\frac{BE}{BC}$=$\frac{1}{3}$，
∴$\frac{EG}{DC}$=$\frac{1}{3}$，
∵D为AC的中点，
∴$\frac{EG}{AD}$=$\frac{1}{3}$，
∴$\frac{EF}{FA}$=$\frac{1}{3}$，
∴$\overrightarrow{AF}$=$\frac{3}{4}$$\overrightarrow{AE}$．
∴实数λ的值为$\frac{3}{4}$，
故答案为：$\frac{3}{4}$．

点评 本题考查平面向量的线性运算以及平行线分线段成比例定理，属于基础题．