
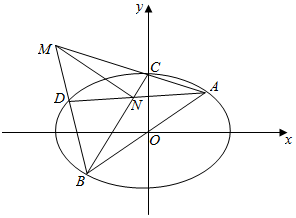
 如图,在平面直角坐标系xOy中,椭圆E的方程为$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1,直线l:y=$\frac{1}{2}$x与椭圆E相交于A,B两点,C,D是椭圆E上异于A,B两点,且直线AC,BD相交于点M,直线AD,BC相交于点N,求证:直线MN的斜率为定值.
如图,在平面直角坐标系xOy中,椭圆E的方程为$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1,直线l:y=$\frac{1}{2}$x与椭圆E相交于A,B两点,C,D是椭圆E上异于A,B两点,且直线AC,BD相交于点M,直线AD,BC相交于点N,求证:直线MN的斜率为定值. 分析 联立$\left\{\begin{array}{l}{y=\frac{1}{2}x}\\{\frac{{x}^{2}}{6}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,解得A(2,1),B(-2,-1).①当CA,CB,DA,DB斜率都存在时,设直线CA,DA的斜率分别为k1,k2,C(x0,y0),显然k1≠k2;可得:k1•kCB=-$\frac{1}{2}$,kCB=-$\frac{1}{2{k}_{1}}$;同理kDB=-$\frac{1}{2{k}_{2}}$,于是直线AD的方程为y-1=k2(x-2),直线BC的方程为y+1=-$\frac{1}{2{k}_{1}}$(x+2);联立解得:点N的坐标为$(\frac{4{k}_{1}{k}_{2}-4{k}_{1}-2}{2{k}_{1}{k}_{2}+1},\frac{-2{k}_{1}{k}_{2}-4{k}_{2}+1}{2{k}_{1}{k}_{2}+1})$;用k2代k1,k1代k2得点M的坐标.可得kMN=$\frac{4({k}_{2}-{k}_{1})}{4({k}_{1}-{k}_{2})}$=-1;即直线MN的斜率为定值-1;②当CA,CB,DA,DB中,有直线的斜率不存在时,根据题设要求,至多有一条直线斜率不存在,故不妨设直线CA的斜率不存在,从而C(2,-1);仍然设DA的斜率为k2,由①知kDB=-$\frac{1}{2{k}_{2}}$;即可得出.
解答 证明:联立$\left\{\begin{array}{l}{y=\frac{1}{2}x}\\{\frac{{x}^{2}}{6}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$,或$\left\{\begin{array}{l}{x=-2}\\{y=-1}\end{array}\right.$,从而A(2,1),B(-2,-1);
①当CA,CB,DA,DB斜率都存在时,设直线CA,DA的斜率分别为k1,k2,C(x0,y0),
显然k1≠k2;
从而k1•kCB=$\frac{{y}_{0}-1}{{x}_{0}-2}$•$\frac{{y}_{0}+1}{{x}_{0}+2}$=$\frac{{y}_{0}^{2}-1}{{x}_{0}^{2}-4}$=$\frac{3(1-\frac{{x}_{0}^{2}}{6})-1}{{x}_{0}^{2}-4}$=-$\frac{1}{2}$,
∴kCB=-$\frac{1}{2{k}_{1}}$;
同理kDB=-$\frac{1}{2{k}_{2}}$,
于是直线AD的方程为y-1=k2(x-2),直线BC的方程为y+1=-$\frac{1}{2{k}_{1}}$(x+2);
由$\left\{\begin{array}{l}{y+1=-\frac{1}{2{k}_{1}}(x+2)}\\{y-1={k}_{2}(x-2)}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{4{k}_{1}{k}_{2}-4{k}_{1}-2}{2{k}_{1}{k}_{2}+1}}\\{y=\frac{-2{k}_{1}{k}_{2}-4{k}_{2}+1}{2{k}_{1}{k}_{2}+1}}\end{array}\right.$,从而点N的坐标为$(\frac{4{k}_{1}{k}_{2}-4{k}_{1}-2}{2{k}_{1}{k}_{2}+1},\frac{-2{k}_{1}{k}_{2}-4{k}_{2}+1}{2{k}_{1}{k}_{2}+1})$;
用k2代k1,k1代k2得点M的坐标为$(\frac{4{k}_{1}{k}_{2}-4{k}_{2}-2}{2{k}_{1}{k}_{2}+1},\frac{-2{k}_{1}{k}_{2}-4{k}_{1}+1}{2{k}_{1}{k}_{2}+1})$.
∴kMN=$\frac{\frac{-2{k}_{1}{k}_{2}-4{k}_{1}+1}{2{k}_{1}{k}_{2}+1}-\frac{-2{k}_{1}{k}_{2}-4{k}_{2}+1}{2{k}_{1}{k}_{2}+1}}{\frac{4{k}_{1}{k}_{2}-4{k}_{2}-2}{2{k}_{1}{k}_{2}+1}-\frac{4{k}_{1}{k}_{2}-4{k}_{1}-2}{2{k}_{1}{k}_{2}+1}}$=$\frac{4({k}_{2}-{k}_{1})}{4({k}_{1}-{k}_{2})}$=-1;
即直线MN的斜率为定值-1;
②当CA,CB,DA,DB中,有直线的斜率不存在时,
根据题设要求,至多有一条直线斜率不存在,
故不妨设直线CA的斜率不存在,从而C(2,-1);
仍然设DA的斜率为k2,由①知kDB=-$\frac{1}{2{k}_{2}}$;
此时CA:x=2,DB:y+1=-$\frac{1}{2{k}_{2}}$(x+2),它们交点M(2,-1-$\frac{2}{{k}_{2}}$);
BC:y=-1,AD:y-1=k2(x-2),它们交点N(2-$\frac{2}{{k}_{2}}$,-1),
从而kMN=-1也成立.
综上可得:kMN=-1为定值.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、斜率计算公式,考查了分类讨论方法、推理能力与计算能力,属于难题.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
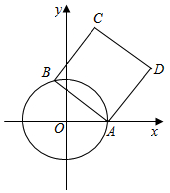 已知圆O为单位圆:x2+y2=1,点A(1,0),B为单位圆上的动点,如图,以AB为边作正方形ABCD,求动点D的轨迹方程及OD的取值范围.
已知圆O为单位圆:x2+y2=1,点A(1,0),B为单位圆上的动点,如图,以AB为边作正方形ABCD,求动点D的轨迹方程及OD的取值范围.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com