
分析 (Ⅰ)当取到的2个球都是红球时,总得分是2分,从而$P(X=2)=\frac{C_k^2}{{C_{k+6}^2}}=\frac{1}{12}$,由此能求出袋子中有3个红球.
(Ⅱ)依题意,X的所有可能取值为2,3,4,6,7,10,分别求出相应的概率,由此能求出X的分布列和数学期望.
解答 (本题13分)
解:(Ⅰ)当取到的2个球都是红球时,总得分是2分,
即$P(X=2)=\frac{C_k^2}{{C_{k+6}^2}}=\frac{1}{12}$,…(2 分)
化简得11k2-23k-30=0,即(k-3)(11k+10)=0,…(3 分)
解得k=3或$k=-\frac{10}{11}$(舍去).
故袋子中有3个红球.…(4 分)
(Ⅱ)依题意,X的所有可能取值为2,3,4,6,7,10.…(5 分)
$P(X=2)=\frac{1}{12}$,
$P(X=3)=\frac{C_3^1C_4^1}{C_9^2}=\frac{3×4}{36}=\frac{1}{3}$,
$P(X=4)=\frac{C_4^2}{C_9^2}=\frac{6}{36}=\frac{1}{6}$,
$P(X=6)=\frac{C_3^1C_2^1}{C_9^2}=\frac{3×2}{36}=\frac{1}{6}$,
$P(X=7)=\frac{C_4^1C_2^1}{C_9^2}=\frac{4×2}{36}=\frac{2}{9}$,
$P(X=10)=\frac{C_2^2}{C_9^2}=\frac{1}{36}$.…(10分)
∴X的分布列为:
| X | 2 | 3 | 4 | 6 | 7 | 10 |
| P | $\frac{1}{12}$ | $\frac{1}{3}$ | $\frac{1}{6}$ | $\frac{1}{6}$ | $\frac{2}{9}$ | $\frac{1}{36}$ |
点评 本题考查概率的求法及应用,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
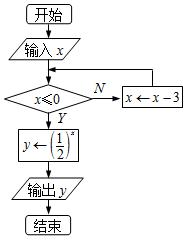 如图,是一个算法的程序框图,当输出的y值为2时,若将输入的x的所有可能值按从小到大的顺序排列得到一个数列{an},则该数列的通项公式为an=an=3n-4.
如图,是一个算法的程序框图,当输出的y值为2时,若将输入的x的所有可能值按从小到大的顺序排列得到一个数列{an},则该数列的通项公式为an=an=3n-4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
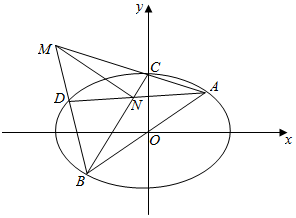 如图,在平面直角坐标系xOy中,椭圆E的方程为$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1,直线l:y=$\frac{1}{2}$x与椭圆E相交于A,B两点,C,D是椭圆E上异于A,B两点,且直线AC,BD相交于点M,直线AD,BC相交于点N,求证:直线MN的斜率为定值.
如图,在平面直角坐标系xOy中,椭圆E的方程为$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1,直线l:y=$\frac{1}{2}$x与椭圆E相交于A,B两点,C,D是椭圆E上异于A,B两点,且直线AC,BD相交于点M,直线AD,BC相交于点N,求证:直线MN的斜率为定值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (-∞,1) | C. | (-1,0)∪(0,3) | D. | (-∞,0)∪(0,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com