
【题目】已知椭圆![]() 过点
过点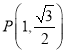 ,设它的左、右焦点分别为
,设它的左、右焦点分别为![]() 、
、![]() ,左顶点为
,左顶点为![]() ,上顶点为
,上顶点为![]() ,且满足
,且满足![]() .
.
(Ⅰ)求椭圆![]() 的标准方程和离心率;
的标准方程和离心率;
(Ⅱ)过点![]() 作不与
作不与![]() 轴垂直的直线交椭圆
轴垂直的直线交椭圆![]() 于
于![]() 、
、![]() (异于点
(异于点![]() )两点,试判断
)两点,试判断![]() 的大小是否为定值,并说明理由.
的大小是否为定值,并说明理由.
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点
的左、右焦点![]() ,离心率为
,离心率为![]() ,点
,点![]() 是椭圆上的动点,
是椭圆上的动点,![]() 的最大面积是
的最大面积是![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)圆E经过椭圆的左、右焦点,且与椭圆![]() 在第一象限的交点为
在第一象限的交点为![]() ,且
,且![]() 三点共线,
三点共线,![]() 为坐标原点,直线
为坐标原点,直线![]() 交椭圆
交椭圆![]() 于两点
于两点![]() ,且
,且![]() .
.
(i) 求直线![]() 的斜率;
的斜率;
(ii)当![]() 的面积取到最大值时,求直线
的面积取到最大值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“牟合方盖”是我国古代数学家刘徽在研究球的体积过程中构造在一个和谐优美的几何体.它由完全相同的四个曲面构成,相对的两个曲面在同一个圆柱的侧面上,好似两个扣合(牟合)在一起的方形伞(方盖),其直观图如图所示,图中四边形是体现其直观性所做的辅助线,当其正视图与侧视图完全相同时,它的正视图和俯视图分别是( )


A.a,bB.a,cC.a,dD.b,d
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年初,我国突发新冠肺炎疫情.面对“突发灾难”,举国上下心,继解放军医疗队于除夕夜飞抵武汉,各省医疗队也陆续增援,纷纷投身疫情防控与病人救治之中.为分担“逆行者”的后顾之忧,某大学学生志愿者团队开展“爱心辅学”活动,为抗疫前线工作者子女在线辅导功课.现随机安排甲、乙、丙3名志愿者为某学生辅导数学、物理、化学、生物4门学科,每名志愿者至少辅导1门学科,每门学科由1名志愿者辅导,则数学学科恰好由甲辅导的概率为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年新冠肺炎疫情期间,某区政府为了解本区居民对区政府防疫工作的满意度,从本区居民中随机抽取若干居民进行评分(满分
年新冠肺炎疫情期间,某区政府为了解本区居民对区政府防疫工作的满意度,从本区居民中随机抽取若干居民进行评分(满分![]() 分).根据调查数据制成如下表格和频率分布直方图.已知评分在
分).根据调查数据制成如下表格和频率分布直方图.已知评分在![]() 的居民有
的居民有![]() 人.
人.
满意度评分 |
|
|
|
|
满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
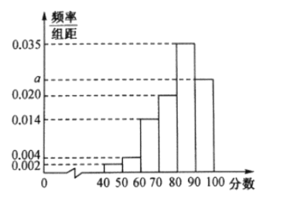
(1)求频率分布直方图中![]() 的值及所调查的总人数;
的值及所调查的总人数;
(2)定义满意度指数![]() (满意程度的平均分)/100,若
(满意程度的平均分)/100,若![]() ,则防疫工作需要进行大的调整,否则不需要大调整.根据所学知识判断该区防疫工作是否需要进行大调整?
,则防疫工作需要进行大的调整,否则不需要大调整.根据所学知识判断该区防疫工作是否需要进行大调整?
(3)为了解部分居民不满意的原因,从不满意的居民(评分在![]() 、
、![]() )中用分层抽样的方法抽取
)中用分层抽样的方法抽取![]() 名居民,倾听他们的意见,并从
名居民,倾听他们的意见,并从![]() 人中抽取
人中抽取![]() 人担任防疫工作的监督员,求这
人担任防疫工作的监督员,求这![]() 人中仅有一人对防疫工作的评分在
人中仅有一人对防疫工作的评分在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四面体![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为其外接球球心,
为其外接球球心,![]() 与
与![]() ,
,![]() ,
,![]() 所成的角分别为
所成的角分别为![]() ,
,![]() ,
,![]() .有下列结论:
.有下列结论:
①该四面体的外接球的表面积为![]() ,
,
②该四面体的体积为10,
③![]()
④![]()
其中所有正确结论的编号为___________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过焦点且垂直于长轴的弦长为
,过焦点且垂直于长轴的弦长为![]() .
.
(1)已知点![]() 是椭圆上两点,点
是椭圆上两点,点![]() 为椭圆的上顶点,
为椭圆的上顶点,![]() 的重心恰好是椭圆的右焦点
的重心恰好是椭圆的右焦点![]() ,求
,求![]() 所
所
在直线的斜率;
(2)过椭圆的右焦点![]() 作直线
作直线![]() ,直线
,直线![]() 与椭圆分别交于点
与椭圆分别交于点![]() ,直线
,直线![]() 与椭圆分别交于点
与椭圆分别交于点![]() ,
,
且![]() ,求四边形
,求四边形![]() 的面积
的面积![]() 最小时直线
最小时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() :
:![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…,对于给定的
,…,对于给定的![]() (
(![]() ,
,![]() ),记满足不等式:
),记满足不等式:![]() (
(![]() ,
,![]() )的
)的![]() 构成的集合为
构成的集合为![]() .
.
(Ⅰ)若数列![]() ,写出集合
,写出集合![]() ;
;
(Ⅱ)如果![]() (
(![]() ,
,![]() )均为相同的单元素集合,求证:数列
)均为相同的单元素集合,求证:数列![]() ,
,![]() ,…,
,…,![]() ,…为等差数列;
,…为等差数列;
(Ⅲ)如果![]() (
(![]() ,
,![]() )为单元素集合,那么数列
)为单元素集合,那么数列![]() ,
,![]() ,…,
,…,![]() ,…还是等差数列吗?如果是等差数列,请给出证明;如果不是等差数列,请给出反例.
,…还是等差数列吗?如果是等差数列,请给出证明;如果不是等差数列,请给出反例.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com