
分析 (Ⅰ)求导,令f′(x)=0时,求得可能的极值点,根据函数单调性与导数的关系,即可求得函数f(x)极值;
(Ⅱ)求得切点,求得切线方程,则$a-b=\frac{e(1-t)}{e^t}-\frac{{e{t^2}}}{e^t}=\frac{{e(-{t^2}-t+1)}}{e^t}$,构造辅助函数,求导,根据导数与函数单调性的关系,函数的F(t)的极大值为F(-1)=e2即为a-b的最大值;
(Ⅲ)设m是方程f[f(x)]=x的解,即f[f(m)]=m,由kAB=-1,则函数f(x)的最大值是1,且f(m)≠m,则$\left\{\begin{array}{l}f(n)=m<1\\ f(m)=n<1\end{array}\right.$,根据函数的单调性,即可求得方程f[f(x)]=x的所有解.
解答 解:(Ⅰ)函数f(x)的导函数为:f′(x)=$\frac{e(1-x)}{{e}^{x}}$;…(1分)
当f′(x)=0时,得x=1;
当f′(x)>0时,得x<1,故函数f(x)在区间(-∞,1)上单调递增;
当f'(x)<0时,得x>1,故函数f(x)在区间(1,+∞)上单调递减;
所以函数f(x)在x=1处取得极大值f(1)=1.…(3分)
(Ⅱ)设函数f(x)的切点为$P(t,\frac{et}{e^t})$,t∈R.
显然该点处的切线为:$y-\frac{et}{e^t}=\frac{e(1-t)}{e^t}(x-t)$,即为$y=\frac{e(1-t)}{e^t}x+\frac{{e{t^2}}}{e^t}$;…(4分)
可得:$\left\{\begin{array}{l}a=\frac{e(1-t)}{e^t}\\ b=\frac{{e{t^2}}}{e^t}\end{array}\right.$,则$a-b=\frac{e(1-t)}{e^t}-\frac{{e{t^2}}}{e^t}=\frac{{e(-{t^2}-t+1)}}{e^t}$;
设函数$F(t)=a-b=\frac{{e(-{t^2}-t+1)}}{e^t}$;…(5分)
其导函数为$F'(t)=\frac{{e({t^2}-t-2)}}{e^t}$,显然函数当F'(t)>0时,得t<-1或t>2,
故函数F(t)在区间(-∞,-1)和(2,+∞)上单调递增;
当F'(t)<0时,得-1<t<2,故函数F(t)在区间(-1,2)上单调递减;
函数的F(t)的极大值为F(-1)=e2>0,F(t)的极小值为$F(2)=-\frac{5}{e}<0$.…(7分)
显然当t∈(-∞,2)时,F(t)≤F(-1)恒成立;
而当t∈(2,+∞)时,$F(t)=e×\frac{{-(t+\frac{1}{2}{)^2}+\frac{5}{4}}}{e^t}$,
其中et>0,$-(t+\frac{1}{2}{)^2}+\frac{5}{4}<-(2+\frac{1}{2}{)^2}+\frac{5}{4}=-5<0$,得F(t)<0;…(8分)
综上所述,函数的F(t)的极大值为F(-1)=e2即为a-b的最大值.…(9分)
(Ⅲ)设m是方程f[f(x)]=x的解,即f[f(m)]=m;
当f(m)=m时,即$\frac{em}{e^m}=m$,可得m=0或m=1;…(11分)
当f(m)≠m时,设f(m)=n,且n≠m.
此时方程f[f(m)]=m,得f(n)=m;
所以两点A(m,n),B(n,m)都在函数f(x)的图象上,且kAB=-1;…(12分)
因为函数f(x)的最大值是1,且f(m)≠m,所以$\left\{\begin{array}{l}f(n)=m<1\\ f(m)=n<1\end{array}\right.$,
因为函数f(x)在区间(-∞,1)上单调递增,两点A(m,n),B(n,m)的横坐标都在区间(-∞,1)上,显然kAB>0; …(13分)
这与kAB=-1相矛盾,此种情况无解;…(14分)
综上,方程f[f(x)]=x的解x=0和x=1.
点评 本题考查导数的综合应用,考查导数与函数单调性及最值得关系,考查转化思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2-2x+2≤0 | B. | ?x0∈R,$x_0^2-2{x_0}+2>0$ | ||
| C. | ?x0∈R,$x_0^2-2{x_0}+2<0$ | D. | ?x0∈R,$x_0^2-2{x_0}+2≤0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
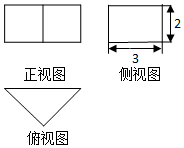
| A. | 18 | B. | $18\sqrt{3}$ | C. | $6\sqrt{3}$ | D. | $12\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{24}π{R^3}$ | B. | $\frac{{\sqrt{3}}}{8}π{R^3}$ | C. | $\frac{{\sqrt{5}}}{24}π{R^3}$ | D. | $\frac{{\sqrt{5}}}{8}π{R^3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com