
| A. | $\frac{{\sqrt{3}}}{24}π{R^3}$ | B. | $\frac{{\sqrt{3}}}{8}π{R^3}$ | C. | $\frac{{\sqrt{5}}}{24}π{R^3}$ | D. | $\frac{{\sqrt{5}}}{8}π{R^3}$ |
分析 推导出设这个盖圆锥形底面半径r=$\frac{R}{2}$,母线长l=R,高h=$\sqrt{{R}^{2}-(\frac{R}{2})^{2}}$=$\frac{\sqrt{3}}{2}R$,由此能求出这个无盖圆锥形容器(不计损耗)的容积.
解答 解:将半径为R的半圆形铁皮制作成一个无盖圆锥形容器,
设这个盖圆锥形底面半径为r,则πR=2πr,解得r=$\frac{R}{2}$,
这个盖圆锥形母线长l=R,
∴这个盖圆锥形的高h=$\sqrt{{R}^{2}-(\frac{R}{2})^{2}}$=$\frac{\sqrt{3}}{2}R$,
∴这个无盖圆锥形容器(不计损耗)的容积:
V=$\frac{1}{3}×S×h$=$\frac{1}{3}×π{r}^{2}×h$
=$\frac{1}{3}×π×(\frac{R}{2})^{2}×\frac{\sqrt{3}}{2}R$
=$\frac{\sqrt{3}}{24}π{R}^{3}$.
故选:A.
点评 本题考查圆锥的容积的求法,考查推理论证能力、运算求解能力,考查等价转化思想、数形结合思想,考查空间思维能力,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{32}$ | B. | $\frac{9}{32}$ | C. | $\frac{31}{32}$ | D. | $\frac{23}{32}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1} | B. | {1,2} | C. | {0,3} | D. | {-1,1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
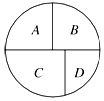 如图所示,用五种不同的颜色分别给A,B,C,D四个区域涂色,相邻区域必须涂不同颜色,若允许同一种颜色多次使用,则不同的涂色方法共有( )种.
如图所示,用五种不同的颜色分别给A,B,C,D四个区域涂色,相邻区域必须涂不同颜色,若允许同一种颜色多次使用,则不同的涂色方法共有( )种.| A. | 120种 | B. | 150 种 | C. | 180 种 | D. | 240 种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -1 | C. | 1 | D. | e |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}$=(1,2,-2),$\overrightarrow{b}$=(-2,-4,1) | B. | $\overrightarrow{a}$=(2,4,5),$\overrightarrow{b}$=(0,0,0) | ||
| C. | $\overrightarrow{a}$=(1,2,$\frac{1}{2}$),$\overrightarrow{b}$=($\frac{1}{2}$,-$\frac{1}{2}$,1) | D. | $\overrightarrow{a}$=(2,4,5),$\overrightarrow{b}$=(-2,-4,-5) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com