
| A. | $\frac{1}{32}$ | B. | $\frac{9}{32}$ | C. | $\frac{31}{32}$ | D. | $\frac{23}{32}$ |
分析 本题利用几何概型求解即可.在a-o-b坐标系中,画出f(1)>0对应 的区域,和a、b都是在区间[0,4]内表示的区域,计算它们的比值即得.
解答  解:f(1)=-1+a-b>0,即a-b>1,
解:f(1)=-1+a-b>0,即a-b>1,
如图,A(1,0),B(4,0),C(4,3),
S△ABC=$\frac{9}{2}$,P=$\frac{\frac{9}{2}}{4×4}$=$\frac{9}{32}$,
故选:B.
点评 本题主要考查几何概型.如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称为几何概型. 古典概型与几何概型的主要区别在于:几何概型是另一类等可能概型,它与古典概型的区别在于试验的结果不是有限个.


科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2-2x+2≤0 | B. | ?x0∈R,$x_0^2-2{x_0}+2>0$ | ||
| C. | ?x0∈R,$x_0^2-2{x_0}+2<0$ | D. | ?x0∈R,$x_0^2-2{x_0}+2≤0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1cm | B. | 2cm | C. | 3cm | D. | $\frac{3}{2}cm$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
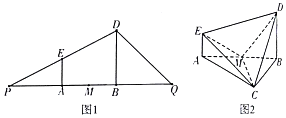 已知△PDQ中,A,B分别为边PQ上的两个三等分点,BD为底边PQ上的高,AE∥DB,如图1,将△PDQ分别沿AE,DB折起,使得P,Q重合于点C.AB中点为M,如图2.
已知△PDQ中,A,B分别为边PQ上的两个三等分点,BD为底边PQ上的高,AE∥DB,如图1,将△PDQ分别沿AE,DB折起,使得P,Q重合于点C.AB中点为M,如图2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
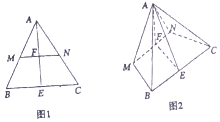 已知在边长为4的等边△ABC(如图1所示)中,MN∥BC,E为BC的中点,连接AE交MN于点F,现将△AMN沿MN折起,使得平面AMN⊥平面MNCB(如图2所示).
已知在边长为4的等边△ABC(如图1所示)中,MN∥BC,E为BC的中点,连接AE交MN于点F,现将△AMN沿MN折起,使得平面AMN⊥平面MNCB(如图2所示).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{24}π{R^3}$ | B. | $\frac{{\sqrt{3}}}{8}π{R^3}$ | C. | $\frac{{\sqrt{5}}}{24}π{R^3}$ | D. | $\frac{{\sqrt{5}}}{8}π{R^3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{20}$ | B. | $\frac{9}{20}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com