
分析 分别令x=1、x=-1,求得 a0+a2+a4+…+a2016 和a1+a3+a7+…+a2017 的值,再利用平方差公式求得${({{a_0}+{a_2}+…+{a_{2016}}})^2}-{({{a_1}+{a_3}+…+{a_{2017}}})^2}$的值.
解答 解:已知${({x-\sqrt{3}})^{2017}}={a_0}{x^{2017}}+{a_1}{x^{2016}}+…+{a_{2016}}x+{a_{2017}}$,
令x=1 可得a0+a1+a2+a3+…+a2016+a2017=${(1-\sqrt{3})}^{2017}$ ①,
x=-1可得a0-a1+a2-a3+…+a2016-a2017=${(-1-\sqrt{3})}^{2017}$ ②,
则${({{a_0}+{a_2}+…+{a_{2016}}})^2}-{({{a_1}+{a_3}+…+{a_{2017}}})^2}$=[( a0+a2+a4+…+a2016 )+(a1+a3+a7+…+a2017 )]
•[(a0+a2+a4+…+a2016 )-( a1+a3+a7+…+a2017 )]
=${(1-\sqrt{3})}^{2017}$•${(-1-\sqrt{3})}^{2017}$=${(-\sqrt{3}+1)}^{2017}$•${(-\sqrt{3}-1)}^{2017}$=(3-1)2017=22017,
故答案为:22017.
点评 本题主要考查二项式定理的应用,是给变量赋值的问题,关键是根据要求的结果,选择合适的数值代入,属于中档题.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 1cm | B. | 2cm | C. | 3cm | D. | $\frac{3}{2}cm$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
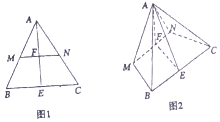 已知在边长为4的等边△ABC(如图1所示)中,MN∥BC,E为BC的中点,连接AE交MN于点F,现将△AMN沿MN折起,使得平面AMN⊥平面MNCB(如图2所示).
已知在边长为4的等边△ABC(如图1所示)中,MN∥BC,E为BC的中点,连接AE交MN于点F,现将△AMN沿MN折起,使得平面AMN⊥平面MNCB(如图2所示).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{24}π{R^3}$ | B. | $\frac{{\sqrt{3}}}{8}π{R^3}$ | C. | $\frac{{\sqrt{5}}}{24}π{R^3}$ | D. | $\frac{{\sqrt{5}}}{8}π{R^3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
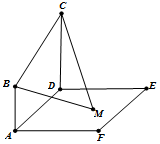 已知平面ABCD⊥平面ADEF,AB⊥AD,CD⊥AD,且AB=1,AD=CD=2.ADEF是正方形,在正方形ADEF内部有一点M,满足MB,MC与平面ADEF所成的角相等,则点M的轨迹长度为$\frac{4}{9}$π.
已知平面ABCD⊥平面ADEF,AB⊥AD,CD⊥AD,且AB=1,AD=CD=2.ADEF是正方形,在正方形ADEF内部有一点M,满足MB,MC与平面ADEF所成的角相等,则点M的轨迹长度为$\frac{4}{9}$π.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com