
分析 依题意,可求得a29=a27=…=a3=a1=1与a6=6,a8=8,…,a30=30,再利用分组求和法即可求得这30天因病请假的总人数.
解答 解:∵a1=1,a2=2,且an+2-an=1+(-1)n (n∈N*),
∴a3-a1=1+(-1)1=0,
∴a3=a1=1,
∴a4-a2=1+(-1)2=2,解得a4=a2+2=4;
同理可得,a29=a27=…=a3=a1=1;
a6=6,a8=8,…,a30=30,
显然,a2、a4、…、a30构成以2为首项,2为公差的等差数列,共15项,
∴这30天因病请假的人数共有:
S30=(a1+a3+…+a29)+(a2+a4+…+a30)=15+$\frac{(2+30)×15}{2}$=255,
故答案为:255.
点评 本题考查数列递推式的应用,求得a29=a27=…=a3=a1=1与a6=6,a8=8,…,a30=30是关键,考查分组求和法的运用,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}$=(1,2,-2),$\overrightarrow{b}$=(-2,-4,1) | B. | $\overrightarrow{a}$=(2,4,5),$\overrightarrow{b}$=(0,0,0) | ||
| C. | $\overrightarrow{a}$=(1,2,$\frac{1}{2}$),$\overrightarrow{b}$=($\frac{1}{2}$,-$\frac{1}{2}$,1) | D. | $\overrightarrow{a}$=(2,4,5),$\overrightarrow{b}$=(-2,-4,-5) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
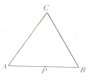 如图,在边长为2的正三角形ABC中,点P从点A出发,沿A→B→C→A的方向前进,然后再回到点A,在此过程中,即点P走过的路程为x,点P到点A,B,C的距离之和为f(x),则函数y=f(x)的大致图象为( )
如图,在边长为2的正三角形ABC中,点P从点A出发,沿A→B→C→A的方向前进,然后再回到点A,在此过程中,即点P走过的路程为x,点P到点A,B,C的距离之和为f(x),则函数y=f(x)的大致图象为( )| A. | 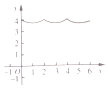 | B. | 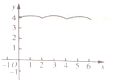 | C. | 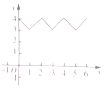 | D. | 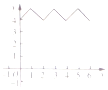 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,e] | B. | [1+$\frac{1}{e}$,e] | C. | (1,e] | D. | (1+$\frac{1}{e}$,e] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com