
分析 (Ⅰ)由题意知A(2t,0),B(0,$\frac{4}{t}$),进而表示出面积即可得到答案.
(Ⅱ)由OM=ON,CM=CN可得OC垂直平分线段MN,根据题意得到直线OC的方程是y=$\frac{1}{2}$x,所以t=2或t=-2,再分别验证t的数值是否正确,进而得到答案.
解答 解:(Ⅰ)证明:由圆C过原点O,且丨OC丨2=t2+$\frac{4}{{t}^{2}}$.
∴圆C的方程是(x-t)2+(y-$\frac{t}{2}$)2=t2+$\frac{4}{{t}^{2}}$.
令x=0,得y1=0,y2=$\frac{4}{t}$;令y=0,得x1=0,x2=2t.
∴△AOB的面积为定值S,S=$\frac{1}{2}$丨OA丨丨OB丨=$\frac{1}{2}$丨$\frac{4}{t}$丨丨2t丨=4,
△AOB的面积为定值4;
(Ⅱ)∵丨OM丨=丨ON丨,丨CM丨=丨CN丨,
∴OC垂直平分线段MN.
∵kMN=-2,kOC=$\frac{1}{2}$,
∴直线OC的方程是y=$\frac{1}{2}$x.
又因为圆心C(t,$\frac{2}{t}$),
∴$\frac{2}{t}$=$\frac{1}{2}$t,解得:t=2或t=-2.
①当t=2时,圆心C的坐标为(2,1),丨OC丨=$\sqrt{5}$,
此时C到直线y=-2x+4的距离d=$\frac{1}{\sqrt{5}}$<$\sqrt{5}$,圆C与直线y=-2x+4相交于两点.
②当t=-2时,圆心C的坐标为(-2,-1),丨OC丨=$\sqrt{5}$,
此时C到直线y=-2x+4的距离d=$\frac{9}{\sqrt{5}}$>$\sqrt{5}$,圆C与直线y=-2x+4不相交,
∴t=-2不符合题意舍去.
∴圆C的方程为(x-2)2+(y-1)2=5.
点评 本题主要考查圆与直线的方程,以及直线与圆的位置关系,并且熟练掌握运用点到直线的距离公式判断直线与圆的位置关系,属于中档题.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:解答题
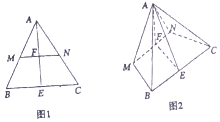 已知在边长为4的等边△ABC(如图1所示)中,MN∥BC,E为BC的中点,连接AE交MN于点F,现将△AMN沿MN折起,使得平面AMN⊥平面MNCB(如图2所示).
已知在边长为4的等边△ABC(如图1所示)中,MN∥BC,E为BC的中点,连接AE交MN于点F,现将△AMN沿MN折起,使得平面AMN⊥平面MNCB(如图2所示).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{20}$ | B. | $\frac{9}{20}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com