
分析 (1)若$f({\frac{1}{2}})+f(2)=0$,代入计算,建立方程,即可求a的值;
(2)利用切线互相垂直,整理得${a^2}-6({{x_0}+\frac{1}{x_0}})a+8{({{x_0}+\frac{1}{x_0}})^2}+5=0$,设f(t)=8t2-6at+a2+5,则f(t)在t∈(2,3)上有零点,考虑到f(2)=32-12a+a2+5=(a-6)2+1>0,所以$\left\{{\begin{array}{l}{2<\frac{3a}{8}<3}\\{f({\frac{3a}{8}})≤0}\end{array}}\right.$或$\left\{{\begin{array}{l}{\frac{3a}{8}≥3}\\{f(3)<0}\end{array}}\right.$,即可解得a的取值范围;
(3)若函数f(x)在区间(1,+∞)上有两个极值点,g(x)在区间(1,+∞)上有两个不同零点,求出a的取值范围,即可得出结论.
解答 解:(1)由$f({\frac{1}{2}})+f(2)=0$得,$({-\frac{1}{4}+\frac{1}{2}a-4ln\frac{1}{2}-a+1})+({-4+2a-4ln2-a+1})=0$,解得$a=\frac{9}{2}$…(3分)
(2)函数f(x)的定义域为(0,+∞),$f'({x_0})=a-2{x_0}-\frac{4}{x_0}$,$f'({\frac{1}{x_0}})=a-\frac{2}{x_0}-4{x_0}$,
由题意得$f'({x_0})f'({\frac{1}{x_0}})=-1$,即$({a-2{x_0}-\frac{4}{x_0}})({a-\frac{2}{x_0}-4{x_0}})=-1$,…(5分)
整理得${a^2}-6({{x_0}+\frac{1}{x_0}})a+8{({{x_0}+\frac{1}{x_0}})^2}+5=0$,
设$t={x_0}+\frac{1}{x_0}$,由${x_0}∈({1,\frac{{3+\sqrt{5}}}{2}})$,得t∈(2,3),
则有8t2-6at+a2+5=0,…(6分)
设f(t)=8t2-6at+a2+5,则f(t)在t∈(2,3)上有零点,考虑到f(2)=32-12a+a2+5=(a-6)2+1>0,
所以$\left\{{\begin{array}{l}{2<\frac{3a}{8}<3}\\{f({\frac{3a}{8}})≤0}\end{array}}\right.$或$\left\{{\begin{array}{l}{\frac{3a}{8}≥3}\\{f(3)<0}\end{array}}\right.$,解得$2\sqrt{10}≤a<8$或8≤a<11,
所以a的取值范围是$[{2\sqrt{10},11})$…(9分)
(3)$f'(x)=-2x+a-\frac{4}{x}=\frac{{-2{x^2}+ax-4}}{x}$,
令g(x)=-2x2+ax-4,由题意,g(x)在区间(1,+∞)上有两个不同零点,
则有$\left\{{\begin{array}{l}{△={a^2}-32>0}\\{\frac{a}{4}>1}\\{g(1)=-6+a<0}\end{array}}\right.$,解得$4\sqrt{2}<a<6$…(10分)
设函数f(x)的两个极值点为x1和x2,
则x1和x2是g(x)在区间(1,+∞)上的两个不同零点,
不妨设x1<x2,则$-2x_2^2+a{x_2}-4=0$①,
得${x_2}=\frac{{a+\sqrt{{a^2}-32}}}{4}$且关于a在$({4\sqrt{2},6})$上递增,
因此${x_2}∈({\sqrt{2},2})$…(12分)
又由①可得$a=2{x_2}+\frac{4}{x_2}$②,
当x∈(1,x1)时,g(x)<0,f'(x)<0,f(x)递减;x∈(x1,x2)时,g(x)>0,f'(x)>0,f(x)递增;
当x∈(x2,+∞)时,g(x)<0,f'(x)<0,f(x)递减,
结合②可得${[{f(x)}]_{极大值}}=f({x_2})=-x_2^2+a{x_2}-4ln{x_2}-a+1=-x_2^2+2x_2^2+4-4ln{x_2}-2{x_2}-\frac{4}{x_2}+1$=$x_2^2-2{x_2}-\frac{4}{x_2}-4ln{x_2}+5,{x_2}∈({\sqrt{2},2})$…(14分)
设$h(x)={x^2}-2x-\frac{4}{x}-4lnx+5,x∈({\sqrt{2},2})$,
则$h'(x)=2x-2+\frac{4}{x^2}-\frac{4}{x}=\frac{{2({x-1})({{x^2}-2})}}{x^2}>0$,
所以h(x)在$({\sqrt{2},2})$上递增,
所以$h({\sqrt{2}})<f({x_2})<h(2)$,从而$h({\sqrt{2}})=7-4\sqrt{2}-2ln2,h(2)=3-4ln2>0$,
所以$f({x_2})∈({7-4\sqrt{2}-2ln2,3-4ln2})$,
又f(1)=0,所以存在m≥3-4ln2,使f(x)<m,
综上,存在满足条件的m,m的取值范围为[3-4ln2,+∞)…(16分)
点评 本题考查导数知识的综合运用,考查函数的零点,考查函数的单调性,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}$=(1,2,-2),$\overrightarrow{b}$=(-2,-4,1) | B. | $\overrightarrow{a}$=(2,4,5),$\overrightarrow{b}$=(0,0,0) | ||
| C. | $\overrightarrow{a}$=(1,2,$\frac{1}{2}$),$\overrightarrow{b}$=($\frac{1}{2}$,-$\frac{1}{2}$,1) | D. | $\overrightarrow{a}$=(2,4,5),$\overrightarrow{b}$=(-2,-4,-5) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
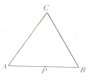 如图,在边长为2的正三角形ABC中,点P从点A出发,沿A→B→C→A的方向前进,然后再回到点A,在此过程中,即点P走过的路程为x,点P到点A,B,C的距离之和为f(x),则函数y=f(x)的大致图象为( )
如图,在边长为2的正三角形ABC中,点P从点A出发,沿A→B→C→A的方向前进,然后再回到点A,在此过程中,即点P走过的路程为x,点P到点A,B,C的距离之和为f(x),则函数y=f(x)的大致图象为( )| A. | 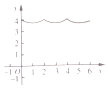 | B. | 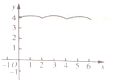 | C. | 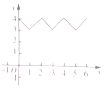 | D. | 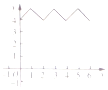 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,e] | B. | [1+$\frac{1}{e}$,e] | C. | (1,e] | D. | (1+$\frac{1}{e}$,e] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
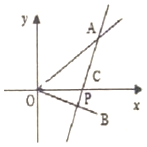 如图,直线OA,OB方程分别为y=x和y=-$\frac{{\sqrt{3}}}{3}$x,过点P(2,0)作直线AB分别交OA,OB于A,B两点,当AB的中点C恰好落在与直线2x+y+m=0,(m∈R)垂直且过原点的直线上时,求直线AB的方程.
如图,直线OA,OB方程分别为y=x和y=-$\frac{{\sqrt{3}}}{3}$x,过点P(2,0)作直线AB分别交OA,OB于A,B两点,当AB的中点C恰好落在与直线2x+y+m=0,(m∈R)垂直且过原点的直线上时,求直线AB的方程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com