
【题目】已知函数![]() .
.
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)设![]() ,若对任意
,若对任意![]() ,均存在
,均存在![]() ,使得
,使得![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)答案见解析;(Ⅱ) ![]() .
.
【解析】试题分析:本题主要考查导数的运算、利用导数研究函数的单调性、利用导数求函数的最值等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,对![]() 求导,对
求导,对![]() 通分,求函数的定义域,讨论
通分,求函数的定义域,讨论![]() 的两个根
的两个根![]() 和2的大小关系,分
和2的大小关系,分![]() 、
、![]() 、
、![]() 、
、![]() 四种情况进行讨论,利用
四种情况进行讨论,利用![]() ,
, ![]() 求函数的单调区间;第二问,先将已知转化为在
求函数的单调区间;第二问,先将已知转化为在![]() 上有
上有![]() ,由已知,
,由已知, ![]() ,下面关键是求
,下面关键是求![]() ,令
,令![]() 即可求出a的取值范围.
即可求出a的取值范围.
试题解析: ![]() .
.
(1)![]() .
.
①当![]() 时,
时, ![]() ,
, ![]() ,在区间(0,2)上,
,在区间(0,2)上, ![]() 在区间
在区间![]() 上
上![]() ,故
,故![]() 的单调递增区间是(0,2),单调递减区间是
的单调递增区间是(0,2),单调递减区间是![]() .
.
②当![]() 时,
时, ![]() ,在区间(0,2)和
,在区间(0,2)和![]() 上,
上, ![]() ;在区间
;在区间![]() 上
上![]() ,故
,故![]() 的单调递增区间是(0,2)和
的单调递增区间是(0,2)和![]() ,单调递减区间是
,单调递减区间是![]() .
.
③当![]() 时,
时, ![]() ,故
,故![]() 的单调递增区间是
的单调递增区间是![]() .
.
④当![]() 时,
时, ![]() ,在区间
,在区间![]() 和
和![]() 上,
上, ![]() ;在区间
;在区间![]() 上,
上, ![]() ,
,
故![]() 的单调递增区间是
的单调递增区间是![]() 和
和![]() ,单调递减区间是
,单调递减区间是![]() .
.
(2)由已知,在![]() 上有
上有![]() .
.
由已知, ![]() ,由(2)可知,
,由(2)可知,
①当![]() 时,
时, ![]() 在
在![]() 上单调递增,
上单调递增,
故![]() ,
,
所以, ![]() ,解得
,解得![]() ,
,
故![]() .
.
②当![]() 时,
时, ![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
故![]() .
.
由![]() 可知
可知![]() ,
, ![]() ,
, ![]() ,
,
所以, ![]() ,
, ![]() ,
,
综上所述, ![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(a+2cos2x)cos(2x+θ)为奇函数,且f( ![]() )=0,其中a∈R,θ∈(0,π).
)=0,其中a∈R,θ∈(0,π).
(1)求a,θ的值;
(2)若f( ![]() )=﹣
)=﹣ ![]() ,α∈(
,α∈( ![]() ,π),求sin(α+
,π),求sin(α+ ![]() )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 关于
关于![]() 轴对称,顶点在坐标原点
轴对称,顶点在坐标原点![]() ,直线
,直线![]() 经过抛物线
经过抛物线![]() 的焦点.
的焦点.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)若不经过坐标原点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相交于不同的两点
相交于不同的两点![]() ,
, ![]() ,且满足
,且满足![]() ,证明直线
,证明直线![]() 过
过![]() 轴上一定点
轴上一定点![]() ,并求出点
,并求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4﹣1:几何证明选讲
如图,AB为⊙O直径,直线CD与⊙O相切与E,AD垂直于CD于D,BC垂直于CD于C,EF垂直于F,连接AE,BE.证明:
(1)∠FEB=∠CEB;
(2)EF2=ADBC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下四个命题:
①如果一条直线和一个平面平行,经过这条直线的一个平面和这个平面相交,那么这条直线和交线平行,
②如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面,
③如果两条直线都平行于一个平面,那么这两条直线互相平行,
④如果一个平面经过另一个平面的一条垂线,那么些两个平面互相垂直.
其中真命题的个数是( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知n为正整数,数列{an}满足an>0,4(n+1)an2﹣nan+12=0,设数列{bn}满足bn= ![]()
(1)求证:数列{ ![]() }为等比数列;
}为等比数列;
(2)若数列{bn}是等差数列,求实数t的值:
(3)若数列{bn}是等差数列,前n项和为Sn , 对任意的n∈N* , 均存在m∈N* , 使得8a12Sn﹣a14n2=16bm成立,求满足条件的所有整数a1的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过原点
经过原点![]() 且与直线
且与直线![]() 相切于点
相切于点![]()
(Ⅰ)求圆![]() 的方程;
的方程;
(Ⅱ)在圆![]() 上是否存在两点
上是否存在两点![]() 关于直线
关于直线![]() 对称,且以线段
对称,且以线段![]() 为直径的圆经过原点?若存在,写出直线
为直径的圆经过原点?若存在,写出直线![]() 的方程;若不存在,请说明理由
的方程;若不存在,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() 中,顶点
中,顶点![]() 在底面的射影为
在底面的射影为![]() .给出下列命题:
.给出下列命题:
①若![]() 、
、![]() 、
、![]() 两两互相垂直,则
两两互相垂直,则![]() 为
为![]() 的垂心;
的垂心;
②若![]() 、
、![]() 、
、![]() 两两互相垂直,则
两两互相垂直,则![]() 有可能为钝角三角形;
有可能为钝角三角形;
③若![]() ,且
,且![]() 与
与![]() 重合,则三棱锥
重合,则三棱锥![]() 的各个面都是直角三角形;
的各个面都是直角三角形;
④若![]() ,且
,且![]() 为
为![]() 边的中点,则
边的中点,则![]() .
.
其中正确命题的序号是__________.(把你认为正确的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中,将底面是直角三角形,且侧棱与底面垂直的三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示(网格纸上正方形的边长为1),则该“堑堵”的表面积为( )
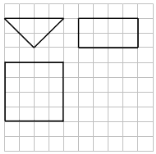
A. 8 B. 16+8![]() C. 16+16
C. 16+16![]() D. 24+16
D. 24+16![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com