
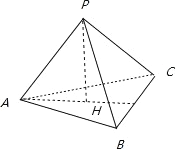
【题目】已知三棱锥![]() 中,顶点
中,顶点![]() 在底面的射影为
在底面的射影为![]() .给出下列命题:
.给出下列命题:
①若![]() 、
、![]() 、
、![]() 两两互相垂直,则
两两互相垂直,则![]() 为
为![]() 的垂心;
的垂心;
②若![]() 、
、![]() 、
、![]() 两两互相垂直,则
两两互相垂直,则![]() 有可能为钝角三角形;
有可能为钝角三角形;
③若![]() ,且
,且![]() 与
与![]() 重合,则三棱锥
重合,则三棱锥![]() 的各个面都是直角三角形;
的各个面都是直角三角形;
④若![]() ,且
,且![]() 为
为![]() 边的中点,则
边的中点,则![]() .
.
其中正确命题的序号是__________.(把你认为正确的序号都填上)
【答案】①③④
【解析】分析:利用线面垂直的判定与性质定理逐一判断即可.
详解:
若PA,PB,PC两两互相垂直,容易推出AH⊥BC,同理BH⊥AC,可得H是△ABC的垂心,①正确;
若![]() 、
、![]() 、
、![]() 两两互相垂直,P在底面是射影H在△ABC的内部,是三角形ABC的垂心,所以不可能是钝角三角形,②不正确;
两两互相垂直,P在底面是射影H在△ABC的内部,是三角形ABC的垂心,所以不可能是钝角三角形,②不正确;
若![]() 与
与![]() 重合则PA⊥平面ABC,所以PA⊥AC,PA⊥AB,PA⊥BC,
重合则PA⊥平面ABC,所以PA⊥AC,PA⊥AB,PA⊥BC,
又BC⊥AC,所以BC⊥平面PAC,所以BC⊥PC,
故四个面都是直角三角形,③正确;
当PH⊥平面ABC时,PA2=PH2+HA2,
PB2=PH2+BH2,PC2=PH2+CH2,
因为H是Rt△ABC斜边AB的中点,所以BH=AH=CH,
故PA=PB=PC,故④正确;


科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为D,且
的定义域为D,且![]() 同时满足以下条件:
同时满足以下条件:
①![]() 在D上是单调递增或单调递减函数;
在D上是单调递增或单调递减函数;
②存在闭区间![]()
![]() D(其中
D(其中![]() ),使得当
),使得当![]() 时,
时,![]() 的取值集合也是
的取值集合也是![]() .那么,我们称函数
.那么,我们称函数![]() (
(![]() )是闭函数.
)是闭函数.
(1)判断![]() 是不是闭函数?若是,找出条件②中的区间;若不是,说明理由.
是不是闭函数?若是,找出条件②中的区间;若不是,说明理由.
(2)若![]() 是闭函数,求实数
是闭函数,求实数![]() 的取值范围.
的取值范围.
(注:本题求解中涉及的函数单调性不用证明,直接指出是增函数还是减函数即可)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O1和圆O2的极坐标方程分别为ρ=2, ![]() .
.
(1)把圆O1和圆O2的极坐标方程化为直角坐标方程;
(2)求经过两圆交点的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读如图所示的程序框图,若输入的k=10,则该算法的功能是( ) 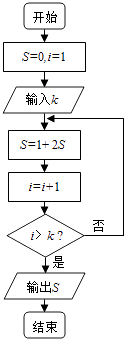
A.计算数列{2n﹣1}的前10项和
B.计算数列{2n﹣1}的前9项和
C.计算数列{2n﹣1}的前10项和
D.计算数列{2n﹣1}的前9项和
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为4,3,则输出v的值为( ) 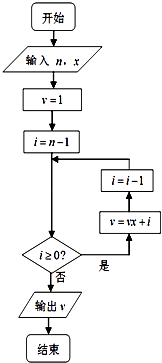
A.20
B.61
C.183
D.548
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某工厂![]() 和
和![]() 两车间工人掌握某技术情况,现从这两车间工人中分别抽查
两车间工人掌握某技术情况,现从这两车间工人中分别抽查![]() 名和
名和![]() 名工人,经测试,将这
名工人,经测试,将这![]() 名工人的测试成绩编成的茎叶图。若成绩在
名工人的测试成绩编成的茎叶图。若成绩在![]() 以上(包括
以上(包括![]() )定义为“良好”,成绩在
)定义为“良好”,成绩在![]() 以下定义为“合格”。已知
以下定义为“合格”。已知![]() 车间工人的成绩的平均数为
车间工人的成绩的平均数为![]() ,
,![]() 车间工人的成绩的中位数为
车间工人的成绩的中位数为![]() .
.

(1)求![]() ,
,![]() 的值;
的值;
(2)求![]() 车间工人的成绩的方差;
车间工人的成绩的方差;
(3)在这![]() 名工人中,用分层抽样的方法从 “良好”和“及格”中抽取
名工人中,用分层抽样的方法从 “良好”和“及格”中抽取![]() 人,再从这
人,再从这![]() 人中选
人中选![]() 人,求至少有一人为“良好”的概率。
人,求至少有一人为“良好”的概率。
(参考公式:方差![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com