
如图,已知四边形 与
与 均为正方形,平面
均为正方形,平面 平面
平面 .
.

(1)求证: 平面
平面 ;
;
(2)求二面角 的大小.
的大小.
(1)详见解析;(2)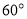 .
.
【解析】
试题分析:(1)要证直线与平面垂直,只须证明这条直线与平面内的两条相交直线垂直或证明这条直线是两垂直平面中一个平面内的一条直线,且这条直线垂直于这两个平面的交线即可.本题属于后者,由平面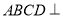 平面
平面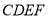 且交线为
且交线为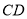 ,而
,而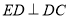 且
且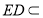 平面
平面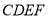 ,所以问题得证;(2)解决空间角最有效的工具是向量法,先以点
,所以问题得证;(2)解决空间角最有效的工具是向量法,先以点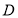 为坐标原点,利用已有的垂直关系建立空间直角坐标系,为计算的方便,不妨设正方形的边长为1,然后标出有效点与有效向量的坐标,易知平面
为坐标原点,利用已有的垂直关系建立空间直角坐标系,为计算的方便,不妨设正方形的边长为1,然后标出有效点与有效向量的坐标,易知平面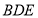 的法向量为
的法向量为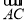 ,再利用待定系数法求出另一平面
,再利用待定系数法求出另一平面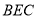 的法向量,接着计算出这两个法向量夹角的余弦值,根据二面角的图形与计算出的余弦值,确定二面角的大小即可.
的法向量,接着计算出这两个法向量夹角的余弦值,根据二面角的图形与计算出的余弦值,确定二面角的大小即可.
试题解析:(1)因为平面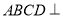 平面
平面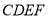 ,且平面
,且平面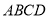
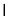 平面
平面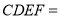
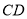
又因为四边形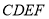 为正方形,所以
为正方形,所以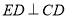
因为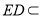 平面
平面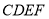 ,所以
,所以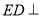 平面
平面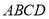 4分
4分
(2)以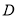 为坐标原点,如图建立空间直角坐标系
为坐标原点,如图建立空间直角坐标系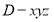
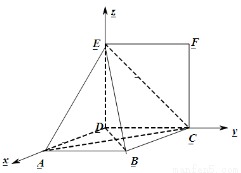
则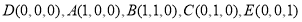
所以平面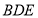 的法向量为
的法向量为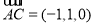 5分
5分
设平面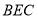 的法向量为
的法向量为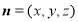
因为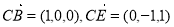
由 得
得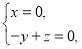 即
即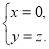
令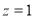 ,则
,则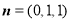 6分
6分
因为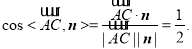
所以二面角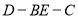 的大小为
的大小为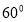 8分.
8分.
考点:1.面面垂直的性质;2.线面垂直的证明;3.空间角的计算.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源:2015届北京市西城区高二第一学期期末理科数学试卷(解析版) 题型:选择题
已知平面内两个定点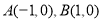 ,过动点
,过动点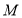 作直线
作直线 的垂线,垂足为
的垂线,垂足为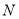 .若
.若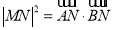 ,则动点
,则动点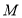 的轨迹是( )
的轨迹是( )
A. 圆 B. 抛物线 C. 椭圆 D. 双曲线
查看答案和解析>>
科目:高中数学 来源:2015届北京东城(南片)高二上学期期末考试理数学试卷(解析版) 题型:填空题
某学校高中部组织赴美游学活动,其中高一240人,高二260人,高三300人,现需按年级抽样分配参加名额40人,高二参加人数为 .
查看答案和解析>>
科目:高中数学 来源:2015届北京东城(南片)高二上学期期末考试文数学试卷(解析版) 题型:填空题
下列命题中,真命题的是 .
①必然事件的概率等于l
②命题“若b=3,则b2=9”的逆命题
③对立事件一定是互斥事件
④命题“相似三角形的对应角相等”的逆否命题
查看答案和解析>>
科目:高中数学 来源:2015届北京东城(南片)高二上学期期末考试文数学试卷(解析版) 题型:选择题
某学校高中部组织赴美游学活动,其中高一240人,高二260人,高三300人,现需按年级抽样分配参加名额40人,高二参加人数为
A. 12 B. 13 C. 14 D. 15
查看答案和解析>>
科目:高中数学 来源:2015届北京东城区高二第一学期期末考试理科数学试卷(解析版) 题型:填空题
一个几何体的三视图如图所示,其中正视图和侧视图是腰长为 的两个全等的等腰直角三角形,则这个几何体的体积为 .
的两个全等的等腰直角三角形,则这个几何体的体积为 .

查看答案和解析>>
科目:高中数学 来源:2015届北京东城区高二第一学期期末考试理科数学试卷(解析版) 题型:选择题
 ,
, 是两个不重合的平面,在下列条件中,可判定
是两个不重合的平面,在下列条件中,可判定 ∥
∥ 的是( )
的是( )
A. ,
, 都与平面
都与平面 垂直
垂直
B. 内不共线的三点到
内不共线的三点到 的距离相等
的距离相等
C. ,
, 是
是 内的两条直线且
内的两条直线且 ∥
∥ ,
, ∥
∥
D. ,
, 是两条异面直线且
是两条异面直线且 ∥
∥ ,
, ∥
∥ ,
, ∥
∥ ,
,  ∥
∥
查看答案和解析>>
科目:高中数学 来源:2015届云南玉溪一中高二上学期期末考试文科数学试卷(解析版) 题型:填空题
下列说法:
① “ ,使
,使 >3”的否定是“
>3”的否定是“ ,使
,使 3”;
3”;
② 函数 的最小正周期是
的最小正周期是 ;
;
③ “在 中,若
中,若 ,则
,则 ”的逆命题是真命题;
”的逆命题是真命题;
④ “ ”是“直线
”是“直线 和直线
和直线 垂直”的充要
垂直”的充要
条件;其中正确的说法是 (只填序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com