
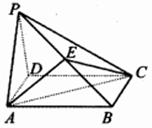
 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠ABC=120°,PA=PD,E为PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠ABC=120°,PA=PD,E为PB的中点.分析 (1)连接BD,交AC于F,连接EF,则EF∥PD,即可证明PD∥面ACE;
(2)建立坐标系,求出平面ACE的一个法向量,利用BD与面ACE所成角为$\frac{π}{3}$,求PB.
解答 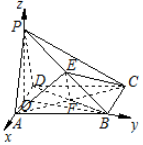 (1)证明:连接BD,交AC于F,连接EF,则EF∥PD.
(1)证明:连接BD,交AC于F,连接EF,则EF∥PD.
∵PD?平面ACE,EF?平面ACE,
∴PD∥平面ACE;
(2)解:设AD 的中点为O,连接PO.
∵PA=PD,∴PO⊥AD,
∵点P在面ABCD的射影在AD上,
∴PO⊥平面ABCD.
∵∠ABC=120°,
∴△ABD为等边三角形,
∴BO⊥AD.
建立如图所示的坐标系,设OP=λ(λ>0),则A(1,0,0),B(0,$\sqrt{3}$,0),C(-2,$\sqrt{3}$,0),D(-1,0,0),E(0,$\frac{\sqrt{3}}{2}$,$\frac{λ}{2}$),
∴$\overrightarrow{BD}$=(-1,-$\sqrt{3}$,0),$\overrightarrow{AC}$=(-3,$\sqrt{3}$,0),$\overrightarrow{AE}$=(-1,$\frac{\sqrt{3}}{2}$,$\frac{λ}{2}$),
设平面ACE的一个法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{-3x+\sqrt{3}y=0}\\{-x+\frac{\sqrt{3}}{2}y+\frac{λ}{2}z=0}\end{array}\right.$,取$\overrightarrow{n}$=(1,$\sqrt{3}$,-$\frac{1}{λ}$),
∵BD与面ACE所成角为$\frac{π}{3}$,
∴$\frac{2}{\sqrt{4+\frac{1}{{λ}^{2}}}}$=$\frac{\sqrt{3}}{2}$,∴λ=$\frac{\sqrt{3}}{2}$,
∴PB=$\sqrt{O{P}^{2}+O{B}^{2}}$=$\frac{\sqrt{15}}{2}$.
点评 本题考查线面平行的判定,考查线面角,考查向量方法的运用,属于中档题.


科目:高中数学 来源: 题型:选择题
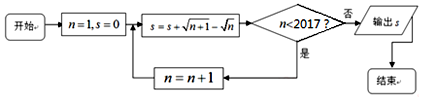
| A. | $\sqrt{2018}-1$ | B. | $\sqrt{2017}-1$ | C. | $\sqrt{2016}-1$ | D. | $\sqrt{2015}-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 积极锻炼身体 | 不积极锻炼身体 | 合计 | |
| 健康状况良好 | 18 | 7 | 25 |
| 健康状况一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
| P(k2>k) | 0.15 | 0.10 | 0.06 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{9}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
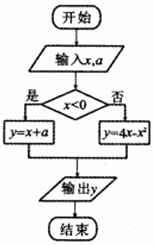
| A. | [-3,4] | B. | [1,4] | C. | [-3,0] | D. | [0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 甲产品所需工时 | 乙产品所需工时 | |
| A设备 | 2 | 3 |
| B设备 | 4 | 1 |
| A. | 40万元 | B. | 45万元 | C. | 50万元 | D. | 55万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 这些女学生的体重和身高具有非线性相关关系 | |
| B. | 这些女学生的体重差异有60%是由身高引起的 | |
| C. | 身高为170cm的学生体重一定为59.5kg | |
| D. | 这些女学生的身高每增加0.85cm,其体重约增加1kg |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {5} | B. | {2} | C. | {2,5} | D. | {5,7} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com