
| A. | 这些女学生的体重和身高具有非线性相关关系 | |
| B. | 这些女学生的体重差异有60%是由身高引起的 | |
| C. | 身高为170cm的学生体重一定为59.5kg | |
| D. | 这些女学生的身高每增加0.85cm,其体重约增加1kg |
分析 根据回归方程$\widehat{y}$=0.85x-85,且刻画回归效果的相关指数R2=0.6,
判断这些女学生的体重和身高具有线性相关关系,
这些女学生的体重差异有60%是由身高引起,
计算x=170时$\widehat{y}$的即可预测结果,
计算身高每增加0.85cm时体重约增加0.85×0.85=0.7225kg.
解答 解:根据回归方程$\widehat{y}$=0.85x-85,且刻画回归效果的相关指数R2=0.6,
所以,这些女学生的体重和身高具有线性相关关系,A错误;
这些女学生的体重差异有60%是由身高引起,B正确;
x=170时,$\widehat{y}$=0.85×170-85=59.5,
预测身高为170cm的学生体重为59.5kg,C错误;
这些女学生的身高每增加0.85cm,其体重约增加0.85×0.85=0.7225kg,D错误.
故选:B.
点评 本题考查了线性回归方程的应用问题,也考查了相关指数的应用问题,是基础题.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案科目:高中数学 来源: 题型:解答题
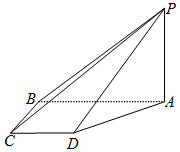 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD是直角梯形,AB⊥BC,AB∥CD,AB=2BC=2CD=2.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD是直角梯形,AB⊥BC,AB∥CD,AB=2BC=2CD=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
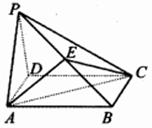 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠ABC=120°,PA=PD,E为PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠ABC=120°,PA=PD,E为PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com