
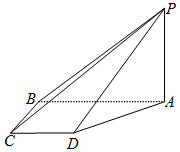
 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD是直角梯形,AB⊥BC,AB∥CD,AB=2BC=2CD=2.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD是直角梯形,AB⊥BC,AB∥CD,AB=2BC=2CD=2.分析 (Ⅰ)证明PA⊥BC,AB⊥BC,即可得BC⊥平面PAB,平面PBC⊥平面PAB
(Ⅱ)以A为原点,AB为x轴、AP为z轴,建立如图所示的空间直角坐标系A-xyz.则B(2,0,0),C(2,1,0),D(1,1,0).设P(0,0,a)(a>0),求出面BPC的法向量$\overrightarrow{{n}_{1}}$及面DPC的法向量$\overrightarrow{{n}_{2}}$,由|cos<$\overrightarrow{{n}_{1}}$,$\overrightarrow{{n}_{2}}$>|=$\frac{|n1•n2|}{|n1||n2|}$=$\frac{2}{\sqrt{(a2+4)(a2+1)}}$=$\frac{\sqrt{2}}{3}$,解得a即可
解答 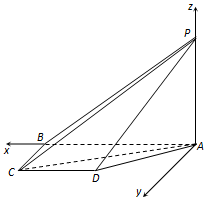 解:(Ⅰ)∵PA⊥平面ABCD,BC?平面ABCD,∴PA⊥BC,
解:(Ⅰ)∵PA⊥平面ABCD,BC?平面ABCD,∴PA⊥BC,
又AB⊥BC,PA∩AB=A,∴BC⊥平面PAB,
∵BC?平面PBC,∴平面PBC⊥平面PAB.…(5分)
(Ⅱ)以A为原点,AB为x轴、AP为z轴,建立如图所示的空间直角坐标系A-xyz.
则B(2,0,0),C(2,1,0),D(1,1,0).
设P(0,0,a)(a>0),
则$\overrightarrow{BC}$=(0,1,0),$\overrightarrow{PC}$=(2,1,-a),
$\overrightarrow{DC}$=(1,0,0)…(8分)
设$\overrightarrow{{n}_{1}}$=(x1,y1,z1)为面BPC的一个法向量,
则$\overrightarrow{{n}_{1}}$•$\overrightarrow{BC}$=$\overrightarrow{{n}_{2}}$•$\overrightarrow{PC}$=0,
即$\left\{\begin{array}{l}y1=0\\ 2x1+y1-az1=0\end{array}$
取x1=a,y1=0,z1=2,得n1=(a,0,2).
同理$\overrightarrow{{n}_{2}}$=(0,a,1)为面DPC的一个法向量.…(10分)
依题意,|cos<$\overrightarrow{{n}_{1}}$,$\overrightarrow{{n}_{2}}$>|=$\frac{|n1•n2|}{|n1||n2|}$=$\frac{2}{\sqrt{(a2+4)(a2+1)}}$=$\frac{\sqrt{2}}{3}$,
解得a2=2,或a2=-7(舍去),所以PA=$\sqrt{2}$. …(12分)
点评 本题考查了面面垂直的判定,向量法处理空间二面角问题的方法,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2]∪(-1,$\frac{3}{2}$) | B. | (-∞,-2]∪(-1,-$\frac{3}{4}$) | C. | (-∞,$\frac{1}{4}$)∪($\frac{1}{4}$,+∞) | D. | (-1,-$\frac{3}{4}$)∪[$\frac{1}{4}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
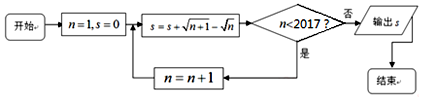
| A. | $\sqrt{2018}-1$ | B. | $\sqrt{2017}-1$ | C. | $\sqrt{2016}-1$ | D. | $\sqrt{2015}-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2i | B. | -2 | C. | i | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 积极锻炼身体 | 不积极锻炼身体 | 合计 | |
| 健康状况良好 | 18 | 7 | 25 |
| 健康状况一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
| P(k2>k) | 0.15 | 0.10 | 0.06 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 这些女学生的体重和身高具有非线性相关关系 | |
| B. | 这些女学生的体重差异有60%是由身高引起的 | |
| C. | 身高为170cm的学生体重一定为59.5kg | |
| D. | 这些女学生的身高每增加0.85cm,其体重约增加1kg |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com