
分析 (1)求出切点坐标(0,0),切线斜率,然后求解切线方程.
(2)令g(x)=f(x)+x2-x,求出g′(x)=ex-1=0,得x=0,判断函数的单调性,求出极小值,然后推出结果.
(3)f(x)>kx对任意的x∈(0,+∞)恒成立$?\frac{f(x)}{x}>k$对任意的x∈(0,+∞)恒成立,构造函数,通过函数的导数求出函数的最小值,然后求出实数k的取值范围.
解答 解:(1)f(x)=ex-x2-1,f′(x)=ex-2x,
∴k=f′(0)=1,
又切点坐标为(0,0),故所求切线方程为y=x;
(2)证明:令g(x)=f(x)+x2-x=ex-x-1,
令g′(x)=ex-1=0,得x=0,
∴当x∈(-∞,0)时,g′(x)<0,g(x)单调递减;
当x∈(0,+∞)时,g′(x)>0,g(x)单调递增.
∴g(x)min=g(0)=0,从而f(x)≥-x2+x.
(3)f(x)>kx对任意的x∈(0,+∞)恒成立$?\frac{f(x)}{x}>k$对任意的x∈(0,+∞)恒成立
令$φ(x)=\frac{f(x)}{x},x>0$,
∴${φ^'}(x)=\frac{{x{f^'}(x)-f(x)}}{x^2}=\frac{{x({e^x}-2x)-({e^x}-{x^2}-1)}}{x^2}=\frac{{(x-1)({e^x}-{x^2}-1)}}{x^2}$
由(2)可知当x∈(0,+∞)时,ex-x-1>0恒成立,
令φ′(x)>0,得x>1;φ′(x)<0,得0<x<1
∴φ(x)的增区间为(1,+∞),减区间为(0,1),φ(x)min=φ(1)=e-2
∴k<φ(x)min=φ(1)=e-2
∴实数k的取值范围是(-∞,e-2).
点评 本题考查函数的最值,函数的单调性以及函数的极值,切线的切线方程的求法,考查计算能力以及转化思想的应用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
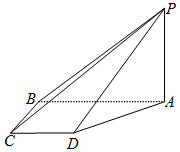 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD是直角梯形,AB⊥BC,AB∥CD,AB=2BC=2CD=2.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD是直角梯形,AB⊥BC,AB∥CD,AB=2BC=2CD=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 若正整数n除以正整数m后的余数为N,则记为n≡N(bmodm),例如10≡4(bmod6),下面程序框图的算法源于我国古代闻名中外的“中国剩余定理”,执行该程序框图,则输出的n等于( )
若正整数n除以正整数m后的余数为N,则记为n≡N(bmodm),例如10≡4(bmod6),下面程序框图的算法源于我国古代闻名中外的“中国剩余定理”,执行该程序框图,则输出的n等于( )| A. | 11 | B. | 13 | C. | 14 | D. | 17 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
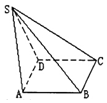 如图:ABCD是菱形,SAD是以AD为底边等腰三角形,$SA=SD=\sqrt{39}$,$AD=2\sqrt{3}$,且二面角S-AD-B大小为120°,∠DAB=60°.
如图:ABCD是菱形,SAD是以AD为底边等腰三角形,$SA=SD=\sqrt{39}$,$AD=2\sqrt{3}$,且二面角S-AD-B大小为120°,∠DAB=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com