
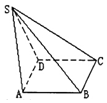
 如图:ABCD是菱形,SAD是以AD为底边等腰三角形,$SA=SD=\sqrt{39}$,$AD=2\sqrt{3}$,且二面角S-AD-B大小为120°,∠DAB=60°.
如图:ABCD是菱形,SAD是以AD为底边等腰三角形,$SA=SD=\sqrt{39}$,$AD=2\sqrt{3}$,且二面角S-AD-B大小为120°,∠DAB=60°.分析 (1)取AD的中点E,连SE,BE,证明AD⊥平面SBE,即可证明:AD⊥SB;
(2)过S作SO⊥直线BE,垂足为O,证明∠SEB为二面角的平面角,再求SC与SAD平面所成角的正弦值.
解答 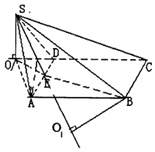 (1)证明:取AD的中点E,连SE,BE,
(1)证明:取AD的中点E,连SE,BE,
由题意知△ABD为正三角形,
∴SE⊥AD,BE⊥AD.
又SE∩BE=E,
∴AD⊥平面SBE,SB?平面SBE,
∴AD⊥SB.
(2)解:过S作SO⊥直线BE,垂足为O,
由(1)知平面ABCD⊥平面SBE,
则SO⊥平面ABCD,连OE,则AD⊥OE.
∴∠SEB为二面角的平面角,∠SEO=60°,
∴$SO=6sin60°=3\sqrt{3}$.
∵BC∥SAD,C到SAD距离为B到SAD距离,
由B作SE垂直BO1,由(1)知平面ASD⊥平面SBE,平面BO1⊥平面SAD,
BE=3,$B{O_1}=2sin60°=\frac{3}{2}\sqrt{3}$.OE=3,EB=3,∴OABD是平行四边形,O在直线CD上,SC2=SO2+OC2=27+48=75,$SC=5\sqrt{3}$.
设线面角为α,$sinα=\frac{{B{O_1}}}{SC}=\frac{3}{10}$,∴SC与平面SAD所成角的正弦值为$\frac{3}{10}$.
点评 本题考查线面垂直的判定与性质,考查线面角,考查学生分析解决问题的能力,属于中档题.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 积极锻炼身体 | 不积极锻炼身体 | 合计 | |
| 健康状况良好 | 18 | 7 | 25 |
| 健康状况一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
| P(k2>k) | 0.15 | 0.10 | 0.06 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,4] | B. | [1,4] | C. | [-3,0] | D. | [0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com