
科目:高中数学 来源: 题型:解答题
(本小题12分)某创业投资公司拟投资开发某种新 能源产品,估计能获得x∈[10,1000]万元的投资收益.现准备制定一个对科研课题组的奖励方案:奖金y(单位:万元)随投资收益x(单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%.
能源产品,估计能获得x∈[10,1000]万元的投资收益.现准备制定一个对科研课题组的奖励方案:奖金y(单位:万元)随投资收益x(单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%.
(Ⅰ)若建立函数f(x)模型制定奖励方案,试用数学语言表述公司对奖励函数f(x)模型
的基本要求;
(Ⅱ)现有两个奖励函数模型:(i) y=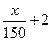 ;(ii) y=4lgx-3.试分析这两个函数模型
;(ii) y=4lgx-3.试分析这两个函数模型
是否符合公司要求?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(14 分)某工厂每天生产某种产品最多不超过40件,并且在生产过程中产品的正品率
分)某工厂每天生产某种产品最多不超过40件,并且在生产过程中产品的正品率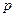 与每日生产产品件数
与每日生产产品件数 (
(
 )间的关系为
)间的关系为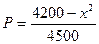 ,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%)
,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%)
(Ⅰ)将日利润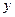 (元)表示成日产量
(元)表示成日产量 (件)的函数;
(件)的函数;
(Ⅱ)求该厂的日产量为多少件时,日利润最大?并求出日利润的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题12分)已知二次函数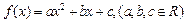 满足:对任意实数x,都有
满足:对任意实数x,都有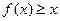 ,且当
,且当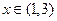 时,有
时,有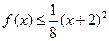 成立.
成立.
(1)求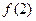 ;
;
(2)若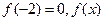 的表达式;
的表达式;
(3)设 ,若
,若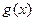 图上的点都位于直线
图上的点都位于直线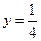 的上方,求实
的上方,求实
数m的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com