
【题目】如图,在平行六面体ABCD-A1B1C1D1中,AA1⊥平面ABCD,且AB=AD=2,AA1=![]() ,∠BAD=120°.
,∠BAD=120°.
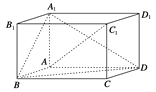
(1)求异面直线A1B与AC1所成角的余弦值;
(2)求二面角B-A1D-A的正弦值.
【答案】(1) ![]() .(2)
.(2) ![]() .
.
【解析】试题分析:(1)先根据条件建立空间直角坐标系,进而得相关点的坐标,求出直线A1B与AC1的方向向量,根据向量数量积求出方向向量夹角,最后根据异面直线所成角与方向向量夹角之间相等或互补可得夹角的余弦值;(2)根据建立的空间直角坐标系,得相关点的坐标,求出各半平面的法向量,根据向量数量积求出法向量的夹角,最后根据二面角与法向量夹角之间关系确定二面角的正弦值.
试题解析:解:在平面ABCD内,过点A作AE![]() AD,交BC于点E.
AD,交BC于点E.
因为AA1![]() 平面ABCD,
平面ABCD,
所以AA1![]() AE,AA1
AE,AA1![]() AD.
AD.
如图,以![]() 为正交基底,建立空间直角坐标系A-xyz.
为正交基底,建立空间直角坐标系A-xyz.
因为AB=AD=2,AA1=![]() ,
, ![]() .
.
则![]() .
.
(1) ![]() ,
,
则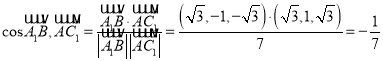 .
.
因此异面直线A1B与AC1所成角的余弦值为![]() .
.
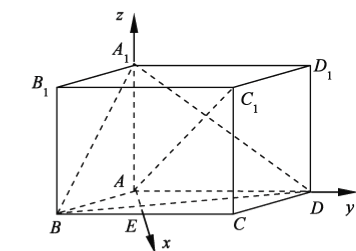
(2)平面A1DA的一个法向量为![]() .
.
设![]() 为平面BA1D的一个法向量,
为平面BA1D的一个法向量,
又![]() ,
,
则![]() 即
即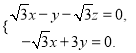
不妨取x=3,则![]() ,
,
所以![]() 为平面BA1D的一个法向量,
为平面BA1D的一个法向量,
从而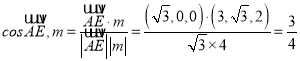 ,
,
设二面角B-A1D-A的大小为![]() ,则
,则![]() .
.
因为![]() ,所以
,所以![]() .
.
因此二面角B-A1D-A的正弦值为![]() .
.
点睛:利用法向量求解空间线面角、面面角的关键在于“四破”:①破“建系关”,构建恰当的空间直角坐标系;②破“求坐标关”,准确求解相关点的坐标;③破“求法向量关”,求出平面的法向量;④破“应用公式关”.


科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,过点
中,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数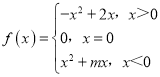 是奇函数,则实数m的值是______;若函数f(x)在区间[-1,a-2]上满足对任意x1≠x2,都有
是奇函数,则实数m的值是______;若函数f(x)在区间[-1,a-2]上满足对任意x1≠x2,都有![]() 成立,则实数a的取值范围是______.
成立,则实数a的取值范围是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求f(x)的定义域;
(2)当x∈(1,+∞),
①求证:f(x)在区间(1,+∞)上是减函数;
②求使关系式f(2+m)>f(2m-1)成立的实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:
①若![]() 是定义在
是定义在![]() 上的偶函数,且在
上的偶函数,且在![]() 上是增函数,
上是增函数,![]() ,则
,则![]() ;
;
②若锐角![]() 、
、![]() 满足c
满足c![]() ,则
,则![]() ;
;
③若![]() ,则
,则![]() 对
对![]() 恒成立;
恒成立;
④要得到![]() 的图像,只需将
的图像,只需将![]() 的图像向右平移
的图像向右平移![]() 个单位:
个单位:
其中真命题的个数有( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的顶点
的顶点![]() ,
, ![]() 在椭圆
在椭圆![]() 上,
上, ![]() 在直线
在直线![]() 上,且
上,且![]() .
.
(![]() )求椭圆
)求椭圆![]() 的离心率.
的离心率.
(![]() )当
)当![]() 边通过坐标原点
边通过坐标原点![]() 时,求
时,求![]() 的长及
的长及![]() 的面积.
的面积.
(![]() )当
)当![]() ,且斜边
,且斜边![]() 的长最大时,求
的长最大时,求![]() 所在直线的方程.
所在直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三年级50名学生参加数学竞赛,根据他们的成绩绘制了如图所示的频率分布直方图,已知分数在![]() 的矩形面积为
的矩形面积为![]() ,
,

求:![]() 分数在
分数在![]() 的学生人数;
的学生人数;
![]() 这50名学生成绩的中位数
这50名学生成绩的中位数![]() 精确到
精确到![]() ;
;
![]() 若分数高于60分就能进入复赛,从不能进入复赛的学生中随机抽取两名,求两人来自不同组的概率.
若分数高于60分就能进入复赛,从不能进入复赛的学生中随机抽取两名,求两人来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的几何体是由以等边三角形![]() 为底面的棱柱被平面
为底面的棱柱被平面![]() 所截而得,已知
所截而得,已知![]() 平面
平面![]()
![]()
![]()
![]() 为
为![]() 的中点,
的中点, ![]() 面
面![]() .
.
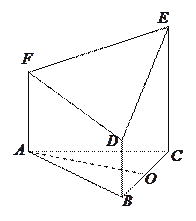
(1)求![]() 的长;
的长;
(2)求证:面![]() 面
面![]() ;
;
(3)求平面![]() 与平面
与平面![]() 相交所成锐角二面角的余弦值.
相交所成锐角二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com